Collisions in Two Dimensions

When two bodies collide, the impulse between them determines the directions in which they then travel. In particular, when the collision is not head-on, the bodies do not end up traveling along their initial axis. For such two-dimensional collisions in a closed, isolated system, the total linear momentum must still be conserved:

If the collision is also elastic (a special case), then the total kinetic energy is also conserved:

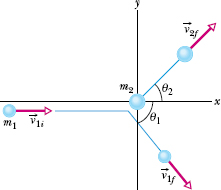
Fig. 9-22   An elastic collision between two bodies in which the collision is not head-on. The body with mass m₂ (the target) is initially at rest.

Equation 9-77 is often more useful for analyzing a two-dimensional collision if we write it in terms of components on an xy coordinate system. For example, Fig. 9-22 shows a glancing collision (it is not head-on) between a projectile body and a target body initially at rest. The impulses between the bodies have sent the bodies off at angles θ₁ and θ₂ to the x axis, along which the projectile initially traveled. In this situation we would rewrite Eq. 9-77 for components along the x axis as

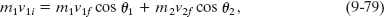
and along the y axis as

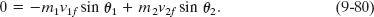
We can also write Eq. 9-78 (for the special case of an elastic collision) in terms of speeds:

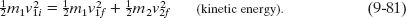
Equations 9-79 to 9-81 contain seven variables: two masses, m₁ and m₂; three speeds, v_1i, v_1f, and v_2f; and two angles, θ₁ and θ₂. If we know any four of these quantities, we can solve the three equations for the remaining three quantities.

CHECKPOINT 11   In Fig. 9-22, suppose that the projectile has an initial momentum of 6 kg · m/s, a final x component of momentum of 4 kg · m/s, and a final y component of momentum of −3 kg · m/s. For the target, what then are (a) the final x component of momentum and (b) the final y component of momentum?