In Lesson 7, we defined work as being energy transferred to or from an object by means of a force acting on the object. We can now extend that definition to an external force acting on a system of objects.
Work is energy transferred to or from a system by means of an external force acting on that system.
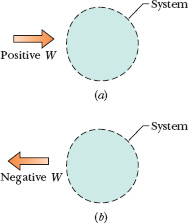
Fig. 8-11 (a) Positive work W done on an arbitrary system means a transfer of energy to the system. (b) Negative work W means a transfer of energy from the system.
Figure 8-11a represents positive work (a transfer of energy to a system), and Fig. 8-11b represents negative work (a transfer of energy from a system). When more than one force acts on a system, their net work is the energy transferred to or from the system.
These transfers are like transfers of money to and from a bank account. If a system consists of a single particle or particle-like object, as in Lesson 7, the work done on the system by a force can change only the kinetic energy of the system. The energy statement for such transfers is the work–kinetic energy theorem of Eq. 7-10 (ΔK = W); that is, a single particle has only one energy account, called kinetic energy. External forces can transfer energy into or out of that account. If a system is more complicated, however, an external force can change other forms of energy (such as potential energy); that is, a more complicated system can have multiple energy accounts.
Let us find energy statements for such systems by examining two basic situations, one that does not involve friction and one that does.
No Friction Involved
To compete in a bowling-ball-hurling contest, you first squat and cup your hands under the ball on the floor. Then you rapidly straighten up while also pulling your hands up sharply, launching the ball upward at about face level. During your upward motion, your applied force on the ball obviously does work; that is, it is an external force that transfers energy, but to what system?
To answer, we check to see which energies change. There is a change ΔK in the ball’s kinetic energy and, because the ball and Earth become more separated, there is a change ΔU in the gravitational potential energy of the ball–Earth system. To include both changes, we need to consider the ball–Earth system. Then your force is an external force doing work on that system, and the work is
where ΔEmec is the change in the mechanical energy of the system. These two equations, which are represented in Fig. 8-12, are equivalent energy statements for work done on a system by an external force when friction is not involved.
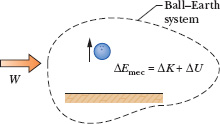
Fig. 8-12 Positive work W is done on a system of a bowling ball and Earth, causing a change ΔEmec in the mechanical energy of the system, a change ΔK in the ball’s kinetic energy, and a change ΔU in the system’s gravitational potential energy.
Friction Involved
We next consider the example in Fig. 8-13a. A constant horizontal force 
pulls a block along an x axis and through a displacement of magnitude d, increasing the block’s velocity from 
to 
. During the motion, a constant kinetic frictional force 
from the floor acts on the block. Let us first choose the block as our system and apply Newton’s second law to it. We can write that law for components along the x axis (Fnet,x = max) as
Because the forces are constant, the acceleration 
is also constant. Thus, we can use Eq. 2-16 to write
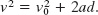
Solving this equation for a, substituting the result into Eq. 8-27, and rearranging then give us
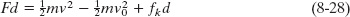
or, because 
for the block,
In a more general situation (say, one in which the block is moving up a ramp), there can be a change in potential energy. To include such a possible change, we generalize Eq. 8-29 by writing
By experiment we find that the block and the portion of the floor along which it slides become warmer as the block slides. As we shall discuss in Lesson 18, the temperature of an object is related to the object’s thermal energy Eth (the energy associated with the random motion of the atoms and molecules in the object). Here, the thermal energy of the block and floor increases because (1) there is friction between them and (2) there is sliding. Recall that friction is due to the cold-welding between two surfaces. As the block slides over the floor, the sliding causes repeated tearing and reforming of the welds between the block and the floor, which makes the block and floor warmer. Thus, the sliding increases their thermal energy Eth.
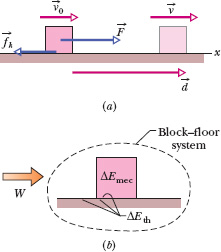
Fig. 8-13 (a) A block is pulled across a floor by force while a kinetic frictional force opposes the motion. The block has velocity at the start of a displacement 
and velocity at the end of the displacement. (b) Positive work W is done on the block–floor system by force , resulting in a change ΔEmec in the block’s mechanical energy and a change ΔEth in the thermal energy of the block and floor.
Through experiment, we find that the increase ΔEth in thermal energy is equal to the product of the magnitudes fk and d:
Thus, we can rewrite Eq. 8-30 as
Fd is the work W done by the external force (the energy transferred by the force), but on which system is the work done (where are the energy transfers made)? To answer, we check to see which energies change. The block’s mechanical energy changes, and the thermal energies of the block and floor also change. Therefore, the work done by force is done on the block–floor system. That work is
This equation, which is represented in Fig. 8-13b, is the energy statement for the work done on a system by an external force when friction is involved.
CHECKPOINT 5 In three trials, a block is pushed by a horizontal applied force across a floor that is not frictionless, as in Fig. 8-13a. The magnitudes F of the applied force and the results of the pushing on the block’s speed are given in the table. In all three trials, the block is pushed through the same distance d. Rank the three trials according to the change in the thermal energy of the block and floor that occurs in that distance d, greatest first.
The prehistoric people of Easter Island carved hundreds of gigantic stone statues in a quarry and then moved them to sites all over the island (Fig. 8-14). How they managed to move the statues by as much as 10 km without the use of sophisticated machines has been hotly debated. They most likely cradled each statue in a wooden sled and then pulled the sled over a “runway” consisting of almost identical logs acting as rollers. In a modern reenactment of this technique, 25 men were able to move a 9000 kg Easter Island-type statue 45 m over level ground in 2 min.
(a) Estimate the work the net force from the men did during the 45 m displacement of the statue, and determine the system on which that force did the work.
Solution: One Key Idea is that we can calculate the work done with Eq. 7-7 (W = Fd cos 
). Here d is the distance 45 m, F is the magnitude of the net force on the statue from the 25 men, and = 0°. Let us estimate that each man pulled with a force magnitude equal to twice his weight, which we take to be the same value mg for all the men. Thus, the magnitude of the net force was F = (25)(2mg) = 50mg. Estimating a man’s mass as 80 kg, we can then write Eq. 7-7 as
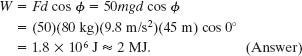
The Key Idea in determining the system on which the work is done is to see which energies change. Because the statue moved, there was certainly a change ΔK in its kinetic energy during the motion. We can easily guess that there must have been considerable kinetic friction between the sled, logs, and ground, resulting in a change ΔEth in their thermal energies. Thus, the system on which the work was done consisted of the statue, sled, logs, and ground.
(b) What was the increase ΔEth in the thermal energy of the system during the 45 m displacement?
Solution: The Key Idea here is that we can relate ΔEth to the work W done by with the energy statement of Eq. 8-33 for a system that involves friction:
Fig. 8-14 Easter Island stone statue.
W = ΔEmec + ΔEth.
We know the value of W from (a). The change ΔEmec in the statue’s mechanical energy was zero because the statue was stationary at the beginning and the end of the move and its elevation did not change. Thus, we find
ΔEth = W = 1.8 × 106 J ≈ 2 MJ. (Answer)
(c) Estimate the work that would have been done by the 25 men if they had moved the statue 10 km across level ground on Easter Island. Also estimate the total change ΔEth that would have occurred in the statue–sled–logs–ground system.
Solution: The Key Ideas here are the same as in (a) and (b). Thus we calculate W as in (a), but with 1 × 104 m now substituted for d. Also, we again equate ΔEth to W. We get
W = ΔEth = 3.9 × 108 J ≈ 400 MJ. (Answer)
This would have been a staggering amount of energy for the men to have transferred during the movement of a statue. Still, the 25 men could have moved the statue 10 km, and the required energy does not suggest some mysterious source.
A food shipper pushes a wood crate of cabbage heads (total mass m = 14 kg) across a concrete floor with a constant horizontal force of magnitude 40 N. In a straight-line displacement of magnitude d = 0.50 m, the speed of the crate decreases from v0 = 0.60 m/s to v = 0.20 m/s.
(a) How much work is done by force , and on what system does it do the work?
Solution: One Key Idea is that Eq. 7-7 holds here: The work W done by can be calculated as
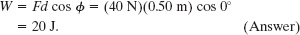
The Key Idea in determining the system on which the work is done is to see which energies change. Because the crate’s speed changes, there is certainly a change ΔK in the crate’s kinetic energy. Is there friction between the floor and the crate, and thus a change in thermal energy? Note that and the crate’s velocity have the same direction. Thus, a Key Idea here is that if there is no friction, then should be accelerating the crate to a greater speed. However, the crate is slowing, so there must be friction and a change ΔEth in thermal energy of the crate and the floor. Therefore, the system on which the work is done is the crate–floor system, because both energy changes occur in that system.
(b) What is the increase ΔEth in the thermal energy of the crate and floor?
Solution: The Key Idea here is that we can relate ΔEth to the work W done by with the energy statement of Eq. 8-33 for a system that involves friction:
We know the value of W from (a). The change ΔEmec in the crate’s mechanical energy is just the change in its kinetic energy because no potential energy changes occur, so we have
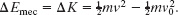
Substituting this into Eq. 8-34 and solving for ΔEth, we find
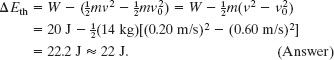
Leave a Reply