Once again we consider a particle that is part of a system in which a conservative force acts. This time suppose that the particle is constrained to move along an x axis while the conservative force does work on it. We can learn a lot about the motion of the particle from a plot of the system’s potential energy U(x). However, before we discuss such plots, we need one more relationship.
Finding the Force Analytically
Equation 8-6 tells us how to find the change ΔU in potential energy between two points in a one-dimensional situation if we know the force F(x). Now we want to go the other way; that is, we know the potential energy function U(x) and want to find the force.
For one-dimensional motion, the work W done by a force that acts on a particle as the particle moves through a distance Δx is F(x) Δx. We can then write Eq. 8-1 as
ΔU(x) = − W = − F(x) Δx.
Solving for F(x) and passing to the differential limit yield
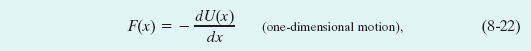
which is the relation we sought.
We can check this result by putting 
, which is the elastic potential energy function for a spring force. Equation 8-22 then yields, as expected, F(x) = − kx, which is Hooke’s law. Similarly, we can substitute U(x) = mgx, which is the gravitational potential energy function for a particle – Earth system, with a particle of mass m at height x above Earth’s surface. Equation 8-22 then yields F = −mg, which is the gravitational force on the particle.
The Potential Energy Curve
Figure 8-10a is a plot of a potential energy function U(x) for a system in which a particle is in one-dimensional motion while a conservative force F(x) does work on it. We can easily find F(x) by (graphically) taking the slope of the U(x) curve at various points. (Equation 8-22 tells us that F(x) is the negative of the slope of the U(x) curve.) Figure 8-10b is a plot of F(x) found in this way.
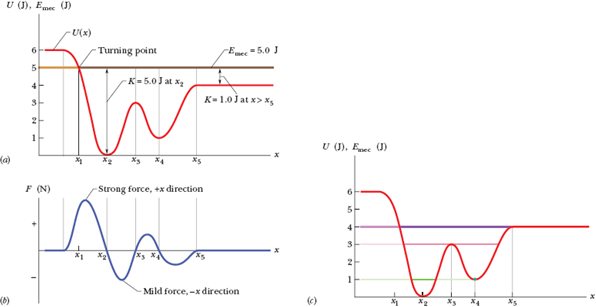
Fig. 8-10 (a) A plot of U(x), the potential energy function of a system containing a particle confined to move along an x axis. There is no friction, so mechanical energy is conserved. (b) A plot of the force F(x) acting on the particle, derived from the potential energy plot by taking its slope at various points. (c) The U(x) plot of (a) with three possible values of Emec shown.
Turning Points
In the absence of a nonconservative force, the mechanical energy E of a system has a constant value given by
Here K(x) is the kinetic energy function of a particle in the system (this K(x) gives the kinetic energy as a function of the particle’s location x). We may rewrite Eq. 8-23 as
Suppose that Emec (which has a constant value, remember) happens to be 5.0 J. It would be represented in Fig. 8-10a by a horizontal line that runs through the value 5.0 J on the energy axis. (It is, in fact, shown there.)
Equation 8-24 tells us how to determine the kinetic energy K for any location x of the particle: On the U(x) curve, find U for that location x and then subtract U from Emec. For example, if the particle is at any point to the right of x5, then K = 1.0 J. The value of K is greatest (5.0 J) when the particle is at x2 and least (0 J) when the particle is at x1.
Since K can never be negative (because v2 is always positive), the particle can never move to the left of x1, where Emec − U is negative. Instead, as the particle moves toward x1 from x2, K decreases (the particle slows) until K = 0 at x1 (the particle stops there).
Note that when the particle reaches x1, the force on the particle, given by Eq. 8-22, is positive (because the slope dU/dx is negative). This means that the particle does not remain at x1 but instead begins to move to the right, opposite its earlier motion. Hence x1 is a turning point, a place where K = 0 (because U = E) and the particle changes direction. There is no turning point (where K = 0) on the right side of the graph. When the particle heads to the right, it will continue indefinitely.
Equilibrium Points
Figure 8-10c shows three different values for Emec superposed on the plot of the potential energy function U(x) of Fig. 8-10a. Let us see how they change the situation. If Emec = 4.0 J (purple line), the turning point shifts from x1 to a point between x1 and x2. Also, at any point to the right of x5, the system’s mechanical energy is equal to its potential energy; thus, the particle has no kinetic energy and (by Eq. 8-22) no force acts on it, and so it must be stationary. A particle at such a position is said to be in neutral equilibrium. (A marble placed on a horizontal tabletop is in that state.)
If Emec = 3.0 J (pink line), there are two turning points: One is between x1 and x2, and the other is between x4 and x5. In addition, x3 is a point at which K = 0. If the particle is located exactly there, the force on it is also zero, and the particle remains stationary. However, if it is displaced even slightly in either direction, a nonzero force pushes it farther in the same direction, and the particle continues to move. A particle at such a position is said to be in unstable equilibrium. (A marble balanced on top of a bowling ball is an example.)
Next consider the particle’s behavior if Emec = 1.0 J (green line). If we place it at x4, it is stuck there. It cannot move left or right on its own because to do so would require a negative kinetic energy. If we push it slightly left or right, a restoring force appears that moves it back to x4. A particle at such a position is said to be in stable equilibrium. (A marble placed at the bottom of a hemispherical bowl is an example.) If we place the particle in the cup-like potential well centered at x2, it is between two turning points. It can still move somewhat, but only partway to x1 or x3.
CHECKPOINT 4 The figure gives the potential energy function U(x) for a system in which a particle is in one-dimensional motion. (a) Rank regions AB, BC, and CD according to the magnitude of the force on the particle, greatest first. (b) What is the direction of the force when the particle is in region AB?
Leave a Reply