The Second Law of Thermodynamics

Here is a puzzle. We saw in Sample Problem 20-1 that if we cause the reversible process of Fig. 20-3 to proceed from (a) to (b) in that figure, the change in entropy of the gas—which we take as our system—is positive. However, because the process is reversible, we can just as easily make it proceed from (b) to (a), simply by slowly adding lead shot to the piston of Fig. 20-3b until the original volume of the gas is restored. In this reverse process, energy must be extracted as heat from the gas to keep its temperature from rising. Hence Q is negative and so, from Eq. 20-2, the entropy of the gas must decrease.

Doesn’t this decrease in the entropy of the gas violate the entropy postulate of Section 20-2, which states that entropy always increases? No, because that postulate holds only for irreversible processes occurring in closed systems. The procedure suggested here does not meet these requirements. The process is not irreversible, and (because energy is transferred as heat from the gas to the reservoir) the system—which is the gas alone—is not closed.

However, if we include the reservoir, along with the gas, as part of the system, then we do have a closed system. Let’s check the change in entropy of the enlarged system gas + reservoir for the process that takes it from (b) to (a) in Fig. 20-3. During this reversible process, energy is transferred as heat from the gas to the reservoir—that is, from one part of the enlarged system to another. Let |Q| represent the absolute value (or magnitude) of this heat. With Eq. 20-2, we can then calculate separately the entropy changes for the gas (which loses |Q|) and the reservoir (which gains |Q|). We get

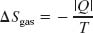
and

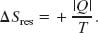
The entropy change of the closed system is the sum of these two quantities, which is zero.

With this result, we can modify the entropy postulate of Section 20-2 to include both reversible and irreversible processes:

 If a process occurs in a closed system, the entropy of the system increases for irreversible processes and remains constant for reversible processes. It never decreases.

Although entropy may decrease in part of a closed system, there will always be an equal or larger entropy increase in another part of the system, so that the entropy of the system as a whole never decreases. This fact is one form of the second law of thermodynamics and can be written as

where the greater-than sign applies to irreversible processes and the equals sign to reversible processes. Equation 20-5 applies only to closed systems.

In the real world almost all processes are irreversible to some extent because of friction, turbulence, and other factors, so the entropy of real closed systems undergoing real processes always increases. Processes in which the system’s entropy remains constant are always idealizations.