The Efficiencies of Real Engines

Let ε_C be the efficiency of a Carnot engine operating between two given temperatures. In this section we prove that no real engine operating between those temperatures can have an efficiency greater than ε_C. If it could, the engine would violate the second law of thermodynamics.

Let us assume that an inventor, working in her garage, has constructed an engine X, which she claims has an efficiency ε_X that is greater than ε_C:

Let us couple engine X to a Carnot refrigerator, as in Fig. 20-15a. We adjust the strokes of the Carnot refrigerator so that the work it requires per cycle is just equal to that provided by engine X. Thus, no (external) work is performed on or by the combination engine + refrigerator of Fig. 20-15a, which we take as our system.

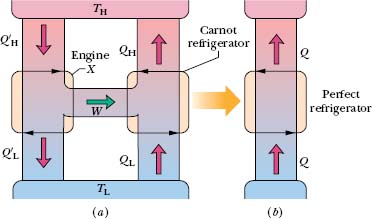
Fig. 20-15 (a) Engine X drives a Carnot refrigerator. (b) If, as claimed, engine X is more efficient than a Carnot engine, then the combination shown in (a) is equivalent to the perfect refrigerator shown here. This violates the second law of thermodynamics, so we conclude that engine X cannot be more efficient than a Carnot engine.

If Eq. 20-15 is true, from the definition of efficiency (Eq. 20-9), we must have

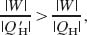
where the prime refers to engine X and the right side of the inequality is the efficiency of the Carnot refrigerator when it operates as an engine. This inequality requires that

Because the work done by engine X is equal to the work done on the Carnot refrigerator, we have, from the first law of thermodynamics as given by Eq. 20-6,

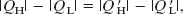
which we can write as

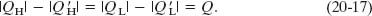
Because of Eq. 20-16, the quantity Q in Eq. 20-17 must be positive.

Comparison of Eq. 20-17 with Fig. 20-15 shows that the net effect of engine X and the Carnot refrigerator working in combination is to transfer energy Q as heat from a low-temperature reservoir to a high-temperature reservoir without the requirement of work. Thus, the combination acts like the perfect refrigerator of Fig. 20-14, whose existence is a violation of the second law of thermodynamics.

Something must be wrong with one or more of our assumptions, and it can only be Eq. 20-15. We conclude that no real engine can have an efficiency greater than that of a Carnot engine when both engines work between the same two temperatures. At most, the real engine can have an efficiency equal to that of a Carnot engine. In that case, the real engine is a Carnot engine.