We saw in Section 17-4 that sound waves are propagated through air and other gases as a series of compressions and expansions; these variations in the transmission medium take place so rapidly that there is no time for energy to be transferred from one part of the medium to another as heat. As we saw in Section 17-11, a process for which Q = 0 is an adiabatic process. We can ensure that Q = 0 either by carrying out the process very quickly (as in sound waves) or by doing it (at any rate) in a well-insulated container. Let us see what the kinetic theory has to say about adiabatic processes.
Figure 19-13a shows our usual insulated cylinder, now containing an ideal gas and resting on an insulating stand. By removing mass from the piston, we can allow the gas to expand adiabatically. As the volume increases, both the pressure and the temperature drop. We shall prove next that the relation between the pressure and the volume during such an adiabatic process is

in which γ = Cp/CV, the ratio of the molar specific heats for the gas. On a p–V diagram such as that in Fig. 19-13b, the process occurs along a line (called an adiabat) that has the equation p = (a constant)/Vγ. Since the gas goes from an initial state i to a final state f, we can rewrite Eq. 19-53 as
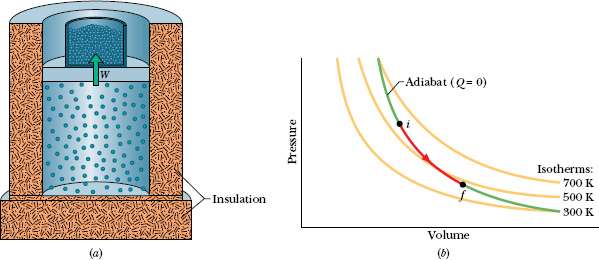
Fig. 19-13 (a) The volume of an ideal gas is increased by removing mass from the piston. The process is adiabatic (Q = 0). (b) The process proceeds from i to f along an adiabat on a p–V diagram.

We can also write an equation for an adiabatic process in terms of T and V. To do so, we use the ideal gas equation (pV = nRT) to eliminate p from Eq. 19-53, finding
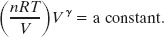
Because n and R are constants, we can rewrite this in the alternative form

in which the constant is different from that in Eq. 19-53. When the gas goes from an initial state i to a final state f, we can rewrite Eq. 19-55 as
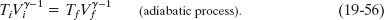
Understanding adiabatic processes allows you to understand why popping the cork on a cold bottle of champagne or the tab on a cold can of soda causes a slight fog to form at the opening of the container. At the top of any unopened carbonated drink sits a gas of carbon dioxide and water vapor. Because the gas pressure is greater than atmospheric pressure, the gas expands out into the atmosphere when the container is opened. Thus, the gas volume increases, but that means the gas must do work pushing against the atmosphere. Because the expansion is rapid, it is adiabatic, and the only source of energy for the work is the internal energy of the gas. Because the internal energy decreases, the temperature of the gas also decreases, which causes the water vapor in the gas to condense into tiny drops of fog. (Note that Eq. 19-56 also tells us that the temperature must decrease during an adiabatic expansion: Vf is greater than Vi, and so Tf must be less than Ti.)
Proof of Eq. 19-53
Suppose that you remove some shot from the piston of Fig. 19-13a, allowing the ideal gas to push the piston and the remaining shot upward and thus to increase the volume by a differential amount dV. Since the volume change is tiny, we may assume that the pressure p of the gas on the piston is constant during the change. This assumption allows us to say that the work dW done by the gas during the volume increase is equal to p dV. From Eq. 18-27, the first law of thermodynamics can then be written as

Since the gas is thermally insulated (and thus the expansion is adiabatic), we substitute 0 for Q. Then we use Eq. 19-45 to substitute nCV dT for dEint. With these substitutions, and after some rearranging, we have

Now from the ideal gas law (pV = nRT) we have

Replacing R with its equal, Cp − CV, in Eq. 19-59 yields

Equating Eqs. 19-58 and 19-60 and rearranging then give
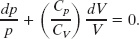
Replacing the ratio of the molar specific heats with γ and integrating (see integral 5 in Appendix E) yield
ln p + γ ln V = a constant.
Rewriting the left side as ln pVγ and then taking the antilog of both sides, we find

which is what we set out to prove.
Free Expansions
Recall from Section 18-11 that a free expansion of a gas is an adiabatic process that involves no work done on or by the gas, and no change in the internal energy of the gas. A free expansion is thus quite different from the type of adiabatic process described by Eqs. 19-53 through 19-61, in which work is done and the internal energy changes. Those equations then do not apply to a free expansion, even though such an expansion is adiabatic.
Also recall that in a free expansion, a gas is in equilibrium only at its initial and final points; thus, we can plot only those points, but not the expansion itself, on a p–V diagram. In addition, because ΔEint = 0, the temperature of the final state must be that of the initial state. Thus, the initial and final points on a p–V diagram must be on the same isotherm, and instead of Eq. 19-56 we have

If we next assume that the gas is ideal (so that pV = nRT), then because there is no change in temperature, there can be no change in the product pV. Thus, instead of Eq. 19-53 a free expansion involves the relation
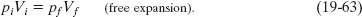
In Sample Problem 19-2, 1 mol of oxygen (assumed to be an ideal gas) expands isothermally (at 310 K) from an initial volume of 12 L to a final volume of 19 L.
(a) What would be the final temperature if the gas had expanded adiabatically to this same final volume? Oxygen (O2) is diatomic and here has rotation but not oscillation.
Solution: The Key Ideas here are as follows:
1. When a gas expands against the pressure of its environment, it must do work.
2. When the process is adiabatic (no energy is transferred as heat), then the energy required for the work can come only from the internal energy of the gas.
3. Because the internal energy decreases, the temperature T must also decrease.
We can relate the initial and final temperatures and volumes with Eq. 19-56:

Because the molecules are diatomic and have rotation but not oscillation, we can take the molar specific heats from Table 19-3. Thus,
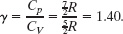
Solving Eq. 19-64 for Tf and inserting known data then yield
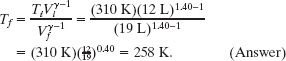
(b) What would be the final temperature and pressure if, instead, the gas had expanded freely to the new volume, from an initial pressure of 2.0 Pa?
Solution: Here the Key Idea is that the temperature does not change in a free expansion:

We find the new pressure using Eq. 19-63, which gives us
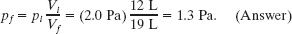
PROBLEM – SOLVING TACTICS
TACTIC 2 : A Graphical Summary of Four Gas Processes
In this lesson we have discussed four special processes that an ideal gas can undergo. An example of each (for a monatomic ideal gas) is shown in Fig. 19-14, and some associated characteristics are given in Table 19-4, including two process names (isobaric and isochoric) that we have not used but that you might see in other courses.
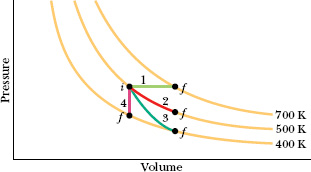
Fig. 19-14 A p–V diagram representing four special processes for an ideal monatomic gas.

![]() CHECKPOINT 5 Rank paths 1, 2, and 3 in Fig. 19-14 according to the energy transfer to the gas as heat, greatest first.
CHECKPOINT 5 Rank paths 1, 2, and 3 in Fig. 19-14 according to the energy transfer to the gas as heat, greatest first.
Leave a Reply