Here is our first kinetic theory problem. Let n moles of an ideal gas be confined in a cubical box of volume V, as in Fig. 19-3. The walls of the box are held at temperature T. What is the connection between the pressure p exerted by the gas on the walls and the speeds of the molecules?
The molecules of gas in the box are moving in all directions and with various speeds, bumping into one another and bouncing from the walls of the box like balls in a racquetball court. We ignore (for the time being) collisions of the molecules with one another and consider only elastic collisions with the walls.
Figure 19-3 shows a typical gas molecule, of mass m and velocity 
, that is about to collide with the shaded wall. Because we assume that any collision of a molecule with a wall is elastic, when this molecule collides with the shaded wall, the only component of its velocity that is changed is the x component, and that component is reversed. This means that the only change in the particle’s momentum is along the x axis, and that change is
Δpx = (−mvx) − (mvx) = −2mvx.
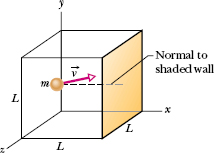
Fig. 19-3 A cubical box of edge length L, containing n moles of an ideal gas. A molecule of mass m and velocity is about to collide with the shaded wall of area L2. A normal to that wall is shown.
Hence, the momentum Δpx delivered to the wall by the molecule during the collision is +2mvx. (Because in this app the symbol p represents both momentum and pressure, we must be careful to note that here p represents momentum and is a vector quantity.)
The molecule of Fig. 19-3 will hit the shaded wall repeatedly. The time Δt between collisions is the time the molecule takes to travel to the opposite wall and back again (a distance 2L) at speed vx. Thus, Δt is equal to 2L/vx. (Note that this result holds even if the molecule bounces off any of the other walls along the way, because those walls are parallel to x and so cannot change vx.) Therefore, the average rate at which momentum is delivered to the shaded wall by this single molecule is
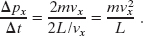
From Newton’s second law 
, the rate at which momentum is delivered to the wall is the force acting on that wall. To find the total force, we must add up the contributions of all the molecules that strike the wall, allowing for the possibility that they all have different speeds. Dividing the magnitude of the total force Fx by the area of the wall (= L2) then gives the pressure p on that wall, where now and in the rest of this discussion, p represents pressure. Thus, using the expression for Δpx/Δt, we can write this pressure as
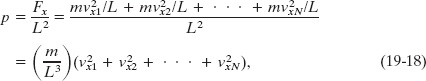
where N is the number of molecules in the box.
Since N = nNA, there are nNA terms in the second set of parentheses of Eq. 19-18. We can replace that quantity by 
, where 
is the average value of the square of the x components of all the molecular speeds. Equation 19-18 then becomes
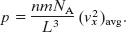
However, mNA is the molar mass M of the gas (that is, the mass of 1 mol of the gas). Also, L3 is the volume of the box, so
For any molecule, 
. Because there are many molecules and because they are all moving in random directions, the average values of the squares of their velocity components are equal, so that 
. Thus, Eq. 19-19 becomes
The square root of (v2)avg is a kind of average speed, called the root-mean-square speed of the molecules and symbolized by vrms. Its name describes it rather well: You square each speed, you find the mean (that is, the average) of all these squared speeds, and then you take the square root of that mean. With 
, we can then write Eq. 19-20 as
Equation 19-21 is very much in the spirit of kinetic theory. It tells us how the pressure of the gas (a purely macroscopic quantity) depends on the speed of the molecules (a purely microscopic quantity).
We can turn Eq. 19-21 around and use it to calculate vrms. Combining Eq. 19-21 with the ideal gas law (pV = nRT) leads to
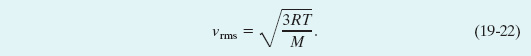
Table 19-1 shows some rms speeds calculated from Eq. 19-22. The speeds are surprisingly high. For hydrogen molecules at room temperature (300 K), the rms speed is 1920 m/s, or 4300 mi/h—faster than a speeding bullet! On the surface of the Sun, where the temperature is 2 × 106 K, the rms speed of hydrogen molecules would be 82 times greater than at room temperature were it not for the fact that at such high speeds, the molecules cannot survive collisions among themselves. Remember too that the rms speed is only a kind of average speed; many molecules move much faster than this, and some much slower.
The speed of sound in a gas is closely related to the rms speed of the molecules of that gas. In a sound wave, the disturbance is passed on from molecule to molecule by means of collisions. The wave cannot move any faster than the “average” speed of the molecules. In fact, the speed of sound must be somewhat less than this “average” molecular speed because not all molecules are moving in exactly the same direction as the wave. As examples, at room temperature, the rms speeds of hydrogen and nitrogen molecules are 1920 m/s and 517 m/s, respectively. The speeds of sound in these two gases at this temperature are 1350 m/s and 350 m/s, respectively.
A question often arises: If molecules move so fast, why does it take as long as a minute or so before you can smell perfume when someone opens a bottle across a room? The answer is that, as we shall discuss in Section 19-6, each perfume molecule may have a high speed but it moves away from the bottle only very slowly because its repeated collisions with other molecules prevent it from moving directly across the room to you.
Here are five numbers: 5, 11, 32, 67, and 89.
(a) What is the average value navg of these numbers?
Solution: We find this from
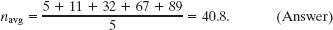
(b) What is the rms value nrms of these numbers?
Solution: We find this from
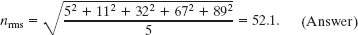
The rms value is greater than the average value because the larger numbers—being squared—are relatively more important in forming the rms value. To test this, let us replace 89 in our set of five numbers by 300. The average value of the new set of five numbers (as you should show) is 2.0 times the previous average value. The rms value, however, is 2.7 times the previous rms value.
Leave a Reply