As Table 19-2 shows, the prediction that 
agrees with experiment for monatomic gases but fails for diatomic and polyatomic gases. Let us try to explain the discrepancy by considering the possibility that molecules with more than one atom can store internal energy in forms other than translational kinetic energy.
Figure 19-11 shows common models of helium (a monatomic molecule, containing a single atom), oxygen (a diatomic molecule, containing two atoms), and methane (a polyatomic molecule). From such models, we would assume that all three types of molecules can have translational motions (say, moving left–right and up–down) and rotational motions (spinning about an axis like a top). In addition, we would assume that the diatomic and polyatomic molecules can have oscillatory motions, with the atoms oscillating slightly toward and away from one another, as if attached to opposite ends of a spring.
To keep account of the various ways in which energy can be stored in a gas, James Clerk Maxwell introduced the theorem of the equipartition of energy:
Every kind of molecule has a certain number f of degrees of freedom, which are independent ways in which the molecule can store energy. Each such degree of freedom has associated with it—on average—an energy of 
kT per molecule (or 
RT per mole).
Let us apply the theorem to the translational and rotational motions of the molecules in Fig. 19-11. (We discuss oscillatory motion in the next section.) For the translational motion, superimpose an xyz coordinate system on any gas. The molecules will, in general, have velocity components along all three axes. Thus, gas molecules of all types have three degrees of translational freedom (three ways to move in translation) and, on average, an associated energy of 
per molecule.
For the rotational motion, imagine the origin of our xyz coordinate system at the center of each molecule in Fig. 19-11. In a gas, each molecule should be able to rotate with an angular velocity component along each of the three axes, so each gas should have three degrees of rotational freedom and, on average, an additional energy of per molecule. However, experiment shows this is true only for the polyatomic molecules. According to quantum theory, the physics dealing with the allowed motions and energies of molecules and atoms, a monatomic gas molecule does not rotate and so has no rotational energy (a single atom cannot rotate like a top). A diatomic molecule can rotate like a top only about axes perpendicular to the line connecting the atoms (the axes are shown in Fig. 19-11b) and not about that line itself. Therefore, a diatomic molecule can have only two degrees of rotational freedom and a rotational energy of only 
per molecule.
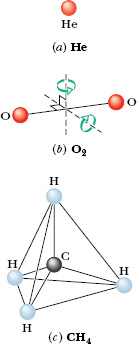
Fig. 19-11 Models of molecules as used in kinetic theory: (a) helium, a typical monatomic molecule; (b) oxygen, a typical diatomic molecule; and (c) methane, a typical polyatomic molecule. The spheres represent atoms, and the lines between them represent bonds. Two rotation axes are shown for the oxygen molecule.
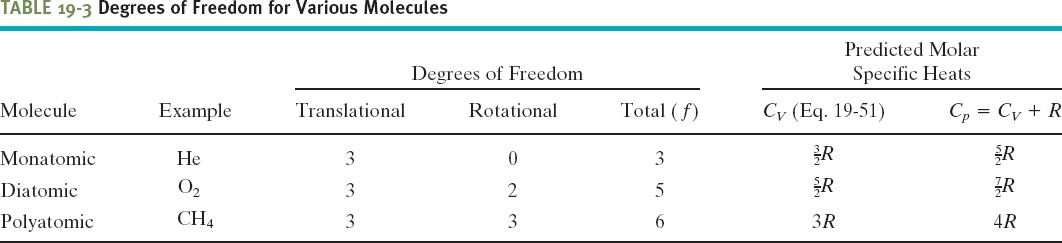
To extend our an alysis of molar specific heats (Cp and CV, in Section 19-8) to ideal diatomic and polyatomic gases, it is necessary to retrace the derivations of that analysis in detail. First, we replace Eq. 19-38 
with Eint = (f/2)nRT, where f is the number of degrees of freedom listed in Table 19-3. Doing so leads to the prediction
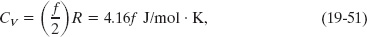
which agrees—as it must—with Eq. 19-43 for monatomic gases (f = 3). As Table 19-2 shows, this prediction also agrees with experiment for diatomic gases (f = 5), but it is too low for polyatomic gases (f = 6 for molecules comparable to CH4).
A cabin of volume V is filled with air (which we consider to be an ideal diatomic gas) at an initial low temperature T1. After you light a wood stove, the air temperature increases to T2. What is the resulting change ΔEint in the internal energy of the air in the cabin?
Solution: As the air temperature increases, the air pressure p cannot change but must always be equal to the air pressure outside the room. The reason is that, because the room is not airtight, the air is not confined. As the temperature increases, air molecules leave through various openings and thus the number of moles n of air in the room decreases. Thus, one Key Idea here is that we cannot use Eq. 19-45 (ΔEint = nCV ΔT) to find ΔEint, because it requires constant n.
A second Key Idea is that we can relate the internal energy Eint at any instant to n and the temperature T with Eq. 19-44 (Eint = nCVT). From that equation we can then write
ΔEint = Δ(nCVT) = CV Δ(nT).
Next, using Eq. 19-5 (pV = nRT), we can replace nT with pV/R, obtaining
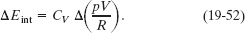
Now, because p, V, and R are all constants, Eq. 19-52 yields
even though the temperature changes.
Why does the cabin feel more comfortable at the higher temperature? There are at least two factors involved: (1) You exchange electromagnetic radiation (thermal radiation) with surfaces inside the room, and (2) you exchange energy with air molecules that collide with you. When the room temperature is increased, (1) the amount of thermal radiation emitted by the surfaces and absorbed by you is increased, and (2) the amount of energy you gain through the collisions of air molecules with you is increased.
Leave a Reply