A Hint of Quantum Theory

We can improve the agreement of kinetic theory with experiment by including the oscillations of the atoms in a gas of diatomic or polyatomic molecules. For example, the two atoms in the O₂ molecule of Fig. 19-11b can oscillate towardand away from each other, with the interconnecting bond acting like a spring. However, experiment shows that such oscillations occur only at relatively high temperatures of the gas—the motion is “turned on” only when the gas molecules have relatively large energies. Rotational motion is also subject to such “turning on,” but at a lower temperature.

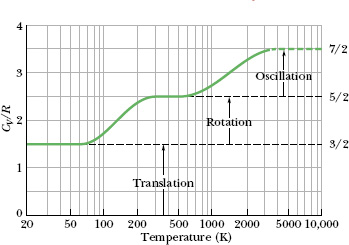
Fig. 19-12 C_V/R versus temperature for (diatomic) hydrogen gas. Because rotational and oscillatory motions begin at certain energies, only translation is possible at very low temperatures. As the temperature increases, rotational motion can begin. At still higher temperatures, oscillatory motion can begin.

Figure 19-12 is of help in seeing this turning on of rotational motion and oscillatory motion. The ratio C_V/R for diatomic hydrogen gas (H₂) is plotted there against temperature, with the temperature scale logarithmic to cover several orders of magnitude. Below about 80 K, we find that C_V/R = 1.5. This result implies that only the three translational degrees of freedom of hydrogen are involved in the specific heat.

As the temperature increases, the value of C_V/R gradually increases to 2.5, implying that two additional degrees of freedom have become involved. Quantum theory shows that these two degrees of freedom are associated with the rotational motion of the hydrogen molecules and that this motion requires a certain minimum amount of energy. At very low temperatures (below 80 K), the molecules do not have enough energy to rotate. As the temperature increases from 80 K, first a few molecules and then more and more obtain enough energy to rotate, and C_V/R increases, until all of them are rotating and C_V/R = 2.5.

Similarly, quantum theory shows that oscillatory motion of the molecules requires a certain (higher) minimum amount of energy. This minimum amount is not met until the molecules reach a temperature of about 1000 K, as shown in Fig. 19-12. As the temperature increases beyond 1000 K, more molecules have enough energy to oscillate and C_V/R increases, until all of them are oscillating and C_V/R = 3.5. (In Fig. 19-12, the plotted curve stops at 3200 K because there the atoms of a hydrogen molecule oscillate so much that they overwhelm their bond, and the molecule then dissociates into two separate atoms.)