So far, we have discussed only the Kelvin scale, used in basic scientific work. In nearly all countries of the world, the Celsius scale (formerly called the centigrade scale) is the scale of choice for popular and commercial use and much scientific use. Celsius temperatures are measured in degrees, and the Celsius degree has the same size as the kelvin. However, the zero of the Celsius scale is shifted to a more convenient value than absolute zero. If TC represents a Celsius temperature and T a Kelvin temperature, then
In expressing temperatures on the Celsius scale, the degree symbol is commonly used. Thus, we write 20.00°C for a Celsius reading but 293.15 K for a Kelvin reading.
The Fahrenheit scale, used in the United States, employs a smaller degree than the Celsius scale and a different zero of temperature. You can easily verify both these differences by examining an ordinary room thermometer on which both scales are marked. The relation between the Celsius and Fahrenheit scales is
where TF is Fahrenheit temperature. Converting between these two scales can be done easily by remembering a few corresponding points, such as the freezing and boiling points of water (Table 18-1). Figure 18-7 compares the Kelvin, Celsius, and Fahrenheit scales.
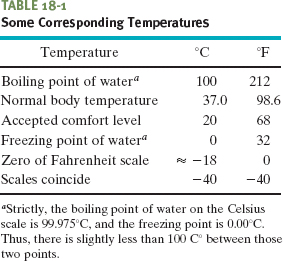
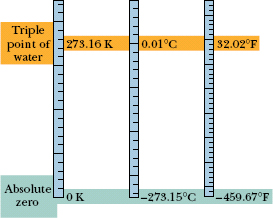
Fig. 18-7 The Kelvin, Celsius, and Fahrenheit temperature scales compared.
We use the letters C and F to distinguish measurements and degrees on the two scales. Thus,
0°C = 32°F
means that 0° on the Celsius scale measures the same temperature as 32° on the Fahrenheit scale, whereas
5 C° = 9 F°
means that a temperature difference of 5 Celsius degrees (note the degree symbol appears after C) is equivalent to a temperature difference of 9 Fahrenheit degrees.
Suppose you come across old scientific notes that describe a temperature scale called Z on which the boiling point of water is 65.0°Z and the freezing point is −14.0°Z. To what temperature on the Fahrenheit scale would a temperature of T = −98.0°Z correspond? Assume that the Z scale is linear; that is, the size of a Z degree is the same everywhere on the Z scale.
Solution: One Key Idea here is to relate the given temperature T to either known temperature on the Z scale. Since T = −98.0°Z is closer to the freezing point (−14.0°Z) than to the boiling point (65.0°Z), we use the freezing point. Then we note that T is below this point by −14.0°Z − (−98.0°Z) = 84.0 Z° (Fig. 18-8). (Read this difference as “84.0 Z degrees.”)
Another Key Idea is to set up a conversion factor between the Z and Fahrenheit scales to convert this difference. To do so, we use both known temperatures on the Z scale and the corresponding temperatures on the Fahrenheit scale. On the Z scale, the difference between the boiling and freezing points is 65.0°Z − (−14.0°Z) = 79.0 Z°. On the Fahrenheit scale, it is 212°F − 32.0°F = 180 F°. Thus, a temperature difference of 79.0 Z° is equivalent to a temperature difference of 180 F° (Fig. 18-8), and we can use the ratio (180 F°)/(79.0 Z°) as our conversion factor.
Now, since T is below the freezing point by 84.0 Z°, it must also be below the freezing point by
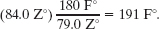
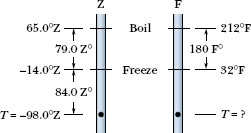
Fig. 18-8 An unknown temperature scale compared with the Fahrenheit temperature scale.
Because the freezing point is at 32.0°F, this means that
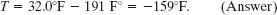
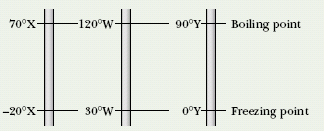
CHECKPOINT 1 The figure here shows three linear temperature scales with the freezing and boiling points of water indicated. (a) Rank the degrees on these scales by size, greatest first. (b) Rank the following temperatures, highest first: 50°X, 50°W, and 50°Y.
PROBLEM – SOLVING TACTICS
TACTIC 1: Temperature Changes
Between the boiling and freezing points of water, there are (approximately) 100 kelvins and 100 Celsius degrees. Thus, a kelvin is the same size as a Celsius degree. From this or from Eq. 18-7, we then know that any temperature change is the same number whether expressed in kelvins or Celsius degrees. For example, a temperature change of 10 K is exactly equivalent to a temperature change of 10 C°.
Between the boiling and freezing points of water, there are 180 Fahrenheit degrees. Thus, 180 F° = 100 K, and a Fahrenheit degree must be 100/180, or 5/9, the size of a kelvin or Celsius degree. From this or from Eq. 18-8, we then know that any temperature change expressed in Fahrenheit degrees must be 
times that same temperature change expressed in either kelvins or Celsius degrees. For example, in Fahrenheit degrees, a temperature change of 10 K is (9/5)(10 K), or 18 F°.
Take care not to confuse a temperature with a temperature change or difference. A temperature of 10 K is certainly not the same as one of 10°C or 18°F but, as noted above, a temperature change of 10 K is the same as one of 10 C° or 18 F°. This distinction is very important in an equation containing a temperature T instead of a temperature change or difference such as T2 − T1: A temperature T by itself should generally be in kelvins and not degrees Celsius or Fahrenheit. In short, beware the “bare T.”
Fig. 18-9 When a Concorde flew faster than the speed of sound, thermal expansion due to the rubbing by passing air increased the aircraft’s length by about 12.5 cm. (The temperature increased to about 128°C at the aircraft nose and about 90°C at the tail, and cabin windows were noticeably warm to the touch.)
Leave a Reply