Heat Capacity
The heat capacity C of an object is the proportionality constant between the heat Q that the object absorbs or loses and the resulting temperature change ΔT of the object; that is,
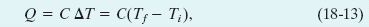
in which Ti and Tf are the initial and final temperatures of the object. Heat capacity C has the unit of energy per degree or energy per kelvin. The heat capacity C of, say, a marble slab used in a bun warmer might be 179 cal/C°, which we can also write as 179 cal/K or as 749 J/K.
The word “capacity” in this context is really misleading in that it suggests analogy with the capacity of a bucket to hold water. That analogy is false, and you should not think of the object as “containing” heat or being limited in its ability to absorb heat. Heat transfer can proceed without limit as long as the necessary temperature difference is maintained. The object may, of course, melt or vaporize during the process.
Specific Heat
Two objects made of the same material—say, marble—will have heat capacities proportional to their masses. It is therefore convenient to define a “heat capacity per unit mass” or specific heat c that refers not to an object but to a unit mass of the material of which the object is made. Equation 18-13 then becomes
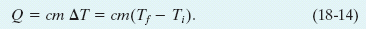
Through experiment we would find that although the heat capacity of a particular marble slab might be 179 cal/C° (or 749 J/K), the specific heat of marble itself (in that slab or in any other marble object) is 0.21 cal/g • C° (or 880 J/kg · K).
From the way the calorie and the British thermal unit were initially defined, the specific heat of water is
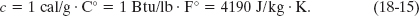
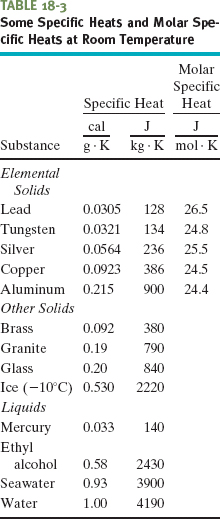
Table 18-3 shows the specific heats of some substances at room temperature. Note that the value for water is relatively high. The specific heat of any substance actually depends somewhat on temperature, but the values in Table 18-3 apply reasonably well in a range of temperatures near room temperature.
CHECKPOINT 3 A certain amount of heat Q will warm 1 g of material A by 3 C° and 1 g of material B by 4 C°. Which material has the greater specific heat?
Molar Specific Heat
In many instances the most convenient unit for specifying the amount of a substance is the mole (mol), where
1 mol = 6.02 × 1023 elementary units
of any substance. Thus 1 mol of aluminum means 6.02 × 1023 atoms (the atom is the elementary unit), and 1 mol of aluminum oxide means 6.02 × 1023 molecules (the molecule is the elementary unit of the compound).
When quantities are expressed in moles, specific heats must also involve moles (rather than a mass unit); they are then called molar specific heats. Table 18-3 shows the values for some elemental solids (each consisting of a single element) at room temperature.
An Important Point
In determining and then using the specific heat of any substance, we need to know the conditions under which energy is transferred as heat. For solids and liquids, we usually assume that the sample is under constant pressure (usually atmospheric) during the transfer. It is also conceivable that the sample is held at constant volume while the heat is absorbed. This means that thermal expansion of the sample is prevented by applying external pressure. For solids and liquids, this is very hard to arrange experimentally, but the effect can be calculated, and it turns out that the specific heats under constant pressure and constant volume for any solid or liquid differ usually by no more than a few percent. Gases, as you will see, have quite different values for their specific heats under constant-pressure conditions and under constant-volume conditions.
Heats of Transformation
When energy is absorbed as heat by a solid or liquid, the temperature of the sample does not necessarily rise. Instead, the sample may change from one phase, or state, to another. Matter can exist in three common states: In the solid state, the molecules of a sample are locked into a fairly rigid structure by their mutual attraction. In the liquid state, the molecules have more energy and move about more. They may form brief clusters, but the sample does not have a rigid structure and can flow or settle into a container. In the gas, or vapor, state, the molecules have even more energy, are free of one another, and can fill up the full volume of a container.
To melt a solid means to change it from the solid state to the liquid state. The process requires energy because the molecules of the solid must be freed from their rigid structure. Melting an ice cube to form liquid water is a common example. To freeze a liquid to form a solid is the reverse of melting and requires that energy be removed from the liquid, so that the molecules can settle into a rigid structure.
To vaporize a liquid means to change it from the liquid state to the vapor (gas) state. This process, like melting, requires energy because the molecules must be freed from their clusters. Boiling liquid water to transfer it to water vapor (or steam—a gas of individual water molecules) is a common example. Condensing a gas to form a liquid is the reverse of vaporizing; it requires that energy be removed from the gas, so that the molecules can cluster instead of flying away from one another.
The amount of energy per unit mass that must be transferred as heat when a sample completely undergoes a phase change is called the heat of transformation L. Thus, when a sample of mass m completely undergoes a phase change, the total energy transferred is

When the phase change is from liquid to gas (then the sample must absorb heat) or from gas to liquid (then the sample must release heat), the heat of transformation is called the heat of vaporization LV. For water at its normal boiling or condensation temperature,
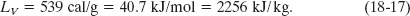
When the phase change is from solid to liquid (then the sample must absorb heat) or from liquid to solid (then the sample must release heat), the heat of transformation is called the heat of fusion LF. For water at its normal freezing or melting temperature,
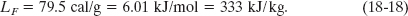
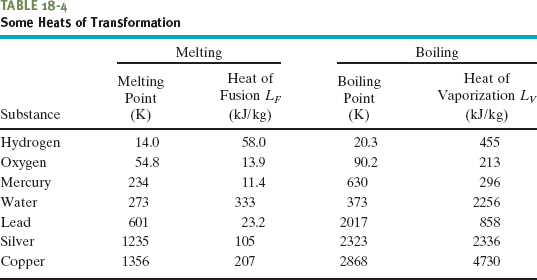
Table 18-4 shows the heats of transformation for some substances.
(a) How much heat must be absorbed by ice of mass m = 720 g at −10°C to take it to liquid state at 15°C?
Solution: The first Key Idea is that the heating process is accomplished in three steps.
Step 1 The Key Idea here is that the ice cannot melt at a temperature below the freezing point—so initially, any energy transferred to the ice as heat can only increase the temperature of the ice. The heat Q1 needed to increase that temperature from the initial value Ti = −10°C to a final value Tf = 0°C (so that the ice can then melt) is given by Eq. 18-14 (Q = cm ΔT). Using the specific heat of ice cice in Table 18-3 gives us
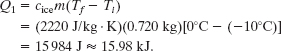
Step 2 The next Key Idea is that the temperature cannot increase from 0°C until all the ice melts—so any energy transferred to the ice as heat now can only change ice to liquid water. The heat Q2 needed to melt all the ice is given by Eq. 18-16 (Q = Lm). Here L is the heat of fusion LF, with the value given in Eq. 18-18 and Table 18-4. We find
Q2 = LF m = (333 kJ/kg)(0.720 kg) ≈ 239.8 kJ.
Step 3 Now we have liquid water at 0°C. The next Key Idea is that the energy transferred to the liquid water as heat now can only increase the temperature of the liquid water. The heat Q3 needed to increase the temperature of the water from the initial value Ti = 0°C to the final value Tf = 15°C is given by Eq. 18-14 (with the specific heat of liquid water cliq
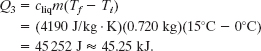
The total required heat Qtot is the sum of the amounts required in the three steps:
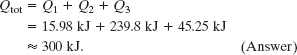
Note that the heat required to melt the ice is much greater than the heat required to raise the temperature of either the ice or the liquid water.
(b) If we supply the ice with a total energy of only 210 kJ (as heat), what then are the final state and temperature of the water?
Solution: From step 1, we know that 15.98 kJ is needed to raise the temperature of the ice to the melting point. The remaining heat Qrem is then 210 kJ − 15.98 kJ, or about 194 kJ. From step 2, we can see that this amount of heat is insufficient to melt all the ice. Then this Key Idea becomes important: Because the melting of the ice is incomplete, we must end up with a mixture of ice and liquid; the temperature of the mixture must be the freezing point, 0°C.
We can find the mass m of ice that is melted by the available energy Qrem by using Eq. 18-16 with LF:
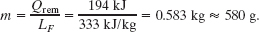
Thus, the mass of the ice that remains is 720 g − 580 g, or 140 g, and we have
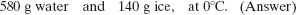
A copper slug whose mass mc is 75 g is heated in a laboratory oven to a temperature T of 312°C. The slug is then dropped into a glass beaker containing a mass mw = 220 g of water. The heat capacity Cb of the beaker is 45 cal/K. The initial temperature Ti of the water and the beaker is 12°C. Assuming that the slug, beaker, and water are an isolated system and the water does not vaporize, find the final temperature Tf of the system at thermal equilibrium.
Solution: One Key Idea here is that, with the system isolated, only internal transfers of energy can occur. There are three such transfers, all as heat. The slug loses energy, the water gains energy, and the beaker gains energy. Another Key Idea is that, because these transfers do not involve a phase change, the energy transfers can only change the temperatures. To relate the transfers to the temperature changes, we can use Eqs. 18-13 and 18-14 to write

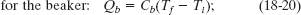
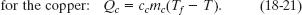
A third Key Idea is that, with the system isolated, the total energy of the system cannot change. This means that the sum of these three energy transfers is zero:
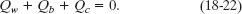
Substituting Eqs. 18-19 through 18-21 into Eq. 18-22 yields
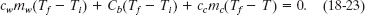
Temperatures are contained in Eq. 18-23 only as differences. Thus, because the differences on the Celsius and Kelvin scales are identical, we can use either of those scales in this equation. Solving it for Tf, we obtain
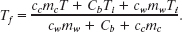
Using Celsius temperatures and taking values for cc and cw from Table 18-3, we find the numerator to be
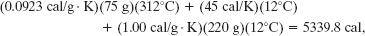
and the denominator to be
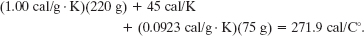
We then have
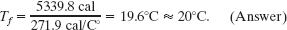
From the given data you can show that
Qw ≈ 1670 cal, Qb ≈ 342 cal, Qc ≈ −2020 cal.
Apart from rounding errors, the algebraic sum of these three heat transfers is indeed zero, as Eq. 18-22 requires.
Leave a Reply