Measuring Temperature

Here we first define and measure temperatures on the Kelvin scale. Then we calibrate a thermoscope so as to make it a thermometer.

The Triple Point of Water

To set up a temperature scale, we pick some reproducible thermal phenomenon and, quite arbitrarily, assign a certain Kelvin temperature to its environment; that is, we select a standard fixed point and give it a standard fixed-point temperature. We could, for example, select the freezing point or the boiling point of water but, for technical reasons, we select instead the triple point of water.

Liquid water, solid ice, and water vapor (gaseous water) can coexist, in thermal equilibrium, at only one set of values of pressure and temperature. Figure 18-4 shows a triple-point cell, in which this so-called triple point of water can be achieved in the laboratory. By international agreement, the triple point of water has been assigned a value of 273.16 K as the standard fixed-point temperature for the calibration of thermometers; that is,

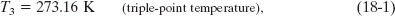
in which the subscript 3 means “triple point.” This agreement also sets the size of the kelvin as 1/273.16 of the difference between absolute zero and the triple-point temperature of water.

Note that we do not use a degree mark in reporting Kelvin temperatures. It is 300 K (not 300°K), and it is read “300 kelvins” (not “300 degrees Kelvin”). The usual SI prefixes apply. Thus, 0.0035 K is 3.5 mK. No distinction in nomenclature is made between Kelvin temperatures and temperature differences, so we can write, “the boiling point of sulfur is 717.8 K” and “the temperature of this water bath was raised by 8.5 K.”

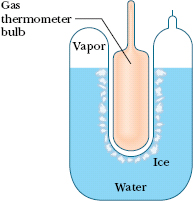
Fig. 18-4   A triple-point cell, in which solid ice, liquid water, and water vapor coexist in thermal equilibrium. By international agreement, the temperature of this mixture has been defined to be 273.16 K. The bulb of a constant-volume gas thermometer is shown inserted into the well of the cell.

The Constant-Volume Gas Thermometer

The standard thermometer, against which all other thermometers are calibrated, is based on the pressure of a gas in a fixed volume. Figure 18-5 shows such a constant-volume gas thermometer; it consists of a gas-filled bulb connected by a tube to a mercury manometer. By raising and lowering reservoir R, the mercury level in the left arm of the U-tube can always be brought to the zero of the scale to keep the gas volume constant (variations in the gas volume can affect temperature measurements).

The temperature of any body in thermal contact with the bulb (such as the liquid surrounding the bulb in Fig. 18-5) is then defined to be

in which p is the pressure exerted by the gas and C is a constant. From Eq. 14-10, the pressure p is

in which p₀ is the atmospheric pressure, ρ is the density of the mercury in the manometer, and h is the measured difference between the mercury levels in the two arms of the tube.* (The minus sign is used in Eq. 18-3 because pressure p is measured above the level at which the pressure is p₀.)

If we next put the bulb in a triple-point cell (Fig. 18-4), the temperature now being measured is

in which p₃ is the gas pressure now. Eliminating C between Eqs. 18-2 and 18-4 gives us the temperature as

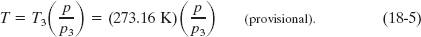
We still have a problem with this thermometer. If we use it to measure, say, the boiling point of water, we find that different gases in the bulb give slightly different results. However, as we use smaller and smaller amounts of gas to fill the bulb, the readings converge nicely to a single temperature, no matter what gas we use. Figure 18-6 shows this convergence for three gases.

Thus the recipe for measuring a temperature with a gas thermometer is

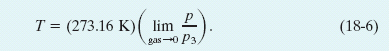
The recipe instructs us to measure an unknown temperature T as follows: Fill the thermometer bulb with an arbitrary amount of any gas (for example, nitrogen) and measure p₃ (using a triple-point cell) and p, the gas pressure at the temperature being measured. (Keep the gas volume the same.) Calculate the ratio p/p₃. Then repeat both measurements with a smaller amount of gas in the bulb, and again calculate this ratio. Continue this way, using smaller and smaller amounts of gas, until you can extrapolate to the ratio p/p₃ that you would find if there were approximately no gas in the bulb. Calculate the temperature T by substituting that extrapolated ratio into Eq. 18-6. (The temperature is called the ideal gas temperature.)

*For pressure units, we shall use units introduced in Section 14-3. The SI unit for pressure is the newton per square meter, which is called the pascal (Pa). The pascal is related to other common pressure units by

1 atm = 1.01 × 10⁵ Pa = 760 torr = 14.7 Ib/in².

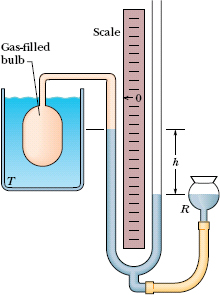
Fig. 18-5   A constant-volume gas thermometer, its bulb immersed in a liquid whose temperature T is to be measured.

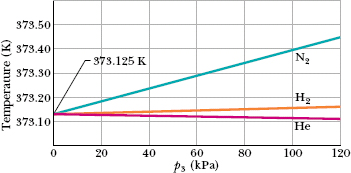
Fig. 18-6   Temperatures measured by a constant-volume gas thermometer, with its bulb immersed in boiling water. For temperature calculations using Eq. 18-5, pressure p₃ was measured at the triple point of water. Three different gases in the thermometer bulb gave generally different results at different gas pressures, but as the amount of gas was decreased (decreasing p₃), all three curves converged to 373.125 K.