A Closer Look at Heat and Work

Here we look in some detail at how energy can be transferred as heat and work between a system and its environment. Let us take as our system a gas confined to a cylinder with a movable piston, as in Fig. 18-13. The upward force on the piston due to the pressure of the confined gas is equal to the weight of lead shot loaded onto the top of the piston. The walls of the cylinder are made of insulating material that does not allow any transfer of energy as heat. The bottom of the cylinder rests on a reservoir for thermal energy, a thermal reservoir (perhaps a hot plate) whose temperature T you can control by turning a knob.

The system (the gas) starts from an initial state i, described by a pressure p_i, a volume V_i, and a temperature T_i. You want to change the system to a final state f, described by a pressure p_f, a volume V_f, and a temperature T_f. The procedure by which you change the system from its initial state to its final state is called a thermodynamic process. During such a process, energy may be transferred into the system from the thermal reservoir (positive heat) or vice versa (negative heat). Also, work can be done by the system to raise the loaded piston (positive work) or lower it (negative work). We assume that all such changes occur slowly, with the result that the system is always in (approximate) thermal equilibrium (that is, every part of the system is always in thermal equilibrium with every other part).

Suppose that you remove a few lead shot from the piston of Fig. 18-13, allowing the gas to push the piston and remaining shot upward through a differential displacement d with an upward force . Since the displacement is tiny, we can assume that  is constant during the displacement. Then  has a magnitude that is equal to pA, where p is the pressure of the gas and A is the face area of the piston. The differential work dW done by the gas during the displacement is

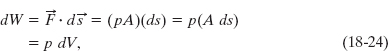
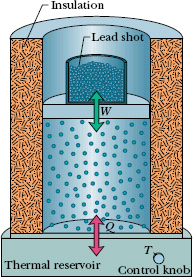
Fig. 18-13   A gas is confined to a cylinder with a movable piston. Heat Q can be added to or withdrawn from the gas by regulating the temperature T of the adjustable thermal reservoir. Work W can be done by the gas by raising or lowering the piston.

in which dV is the differential change in the volume of the gas due to the movement of the piston. When you have removed enough shot to allow the gas to change its volume from V_i to V_f, the total work done by the gas is

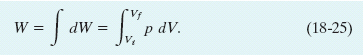
During the change in volume, the pressure and temperature of the gas may also change. To evaluate the integral in Eq. 18-25 directly, we would need to know how pressure varies with volume for the actual process by which the system changes from state i to state f.

There are actually many ways to take the gas from state i to state f. One way is shown in Fig. 18-14a, which is a plot of the pressure of the gas versus its volume and which is called a p–V diagram. In Fig. 18-14a, the curve indicates that the pressure decreases as the volume increases. The integral in Eq. 18-25 (and thus the work W done by the gas) is represented by the shaded area under the curve between points i and f. Regardless of what exactly we do to take the gas along the curve, that work is positive, due to the fact that the gas increases its volume by forcing the piston upward.

Another way to get from state i to state f is shown in Fig. 18-14b. There the change takes place in two steps—the first from state i to state a, and the second from state a to state f.

Step ia of this process is carried out at constant pressure, which means that you leave undisturbed the lead shot that ride on top of the piston in Fig. 18-13. You cause the volume to increase (from V_i to V_f) by slowly turning up the temperature control knob, raising the temperature of the gas to some higher value T_a. (Increasing the temperature increases the force from the gas on the piston, moving it upward.) During this step, positive work is done by the expanding gas (to lift the loaded piston) and heat is absorbed by the system from the thermal reservoir (in response to the arbitrarily small temperature differences that you create as you turn up the temperature). This heat is positive because it is added to the system.

Step af of the process of Fig. 18-14b is carried out at constant volume, so you must wedge the piston, preventing it from moving. Then as you use the control knob to decrease the temperature, you find that the pressure drops from p_a to its final value p_f. During this step, heat is lost by the system to the thermal reservoir.

For the overall process iaf, the work W, which is positive and is carried out only during step ia, is represented by the shaded area under the curve. Energy is transferred as heat during both steps ia and af, with a net energy transfer Q.

Figure 18-14c shows a process in which the previous two steps are carried out in reverse order. The work W in this case is smaller than for Fig. 18-14b, as is the net heat absorbed. Figure 18-14d suggests that you can make the work done by the gas as small as you want (by following a path like icdf) or as large as you want (by following a path like ighf).

To sum up: A system can be taken from a given initial state to a given final state by an infinite number of processes. Heat may or may not be involved, and in general, the work W and the heat Q will have different values for different processes. We say that heat and work are path-dependent quantities.

Fig. 18-14   (a) The shaded area represents the work W done by a system as it goes from an initial state i to a final state f. Work W is positive because the system’s volume increases. (b) W is still positive, but now greater. (c) W is still positive, but now smaller. (d) W can be even smaller (path icdf) or larger (path ighf). (e) Here the system goes from state f to state i as the gas is compressed to less volume by an external force. The work W done by the system is now negative. (f) The net work W_net done by the system during a complete cycle is represented by the shaded area.

Figure 18-14e shows an example in which negative work is done by a system as some external force compresses the system, reducing its volume. The absolute value of the work done is still equal to the area beneath the curve, but because the gas is compressed, the work done by the gas is negative.

Figure 18-14f shows a thermodynamic cycle in which the system is taken from some initial state i to some other state f and then back to i. The net work done by the system during the cycle is the sum of the positive work done during the expansion and the negative work done during the compression. In Fig. 18-14f, the net work is positive because the area under the expansion curve (i to f) is greater than the area under the compression curve (f to i).

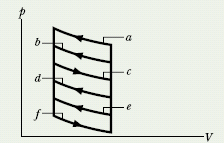
 CHECKPOINT 4 The p–V diagram here shows six curved paths (connected by vertical paths) that can be followed by a gas. Which two of the curved paths should be part of a closed cycle (those curved paths plus connecting vertical paths) if the net work done by the gas during the cycle is to be at its maximum positive value?