Musical sounds can be set up by oscillating strings (guitar, piano, violin), membranes (kettledrum, snare drum), air columns (flute, oboe, pipe organ, and the horns of Fig. 17-13), wooden blocks or steel bars (marimba, xylophone), and many other oscillating bodies. Most instruments involve more than a single oscillating part. In the violin, for example, both the strings and the body of the instrument participate in producing the music.
Recall from Lesson 16 that standing waves can be set up on a stretched string that is fixed at both ends. They arise because waves traveling along the string are reflected back onto the string at each end. If the wavelength of the waves is suitably matched to the length of the string, the superposition of waves traveling in opposite directions produces a standing wave pattern (or oscillation mode). The wavelength required of the waves for such a match is one that corresponds to a resonant frequency of the string. The advantage of setting up standing waves is that the string then oscillates with a large, sustained amplitude, pushing back and forth against the surrounding air and thus generating a noticeable sound wave with the same frequency as the oscillations of the string. This production of sound is of obvious importance to, say, a guitarist.

Fig. 17-13 The air column within a horn oscillates when the instrument is played.
We can set up standing waves of sound in an air-filled pipe in a similar way. As sound waves travel through the air in the pipe, they are reflected at each end and travel back through the pipe. (The reflection occurs even if an end is open, but the reflection is not as complete as when the end is closed.) If the wavelength of the sound waves is suitably matched to the length of the pipe, the superposition of waves traveling in opposite directions through the pipe sets up a standing wave pattern. The wavelength required of the sound waves for such a match is one that corresponds to a resonant frequency of the pipe. The advantage of such a standing wave is that the air in the pipe oscillates with a large, sustained amplitude, emitting at any open end a sound wave that has the same frequency as the oscillations in the pipe. This emission of sound is of obvious importance to, say, an organist.
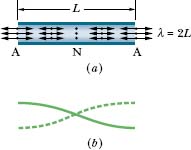
Fig. 17-14 (a) The simplest standing wave pattern of displacement for (longitudinal) sound waves in a pipe with both ends open has an antinode (A) across each end and a node (N) across the middle. (The longitudinal displacements represented by the double arrows are greatly exaggerated.) (b) The corresponding standing wave pattern for (transverse) string waves.
Many other aspects of standing sound wave patterns are similar to those of string waves: The closed end of a pipe is like the fixed end of a string in that there must be a node (zero displacement) there, and the open end of a pipe is like the end of a string attached to a freely moving ring, as in Fig. 16-21b, in that there must be an antinode there. (Actually, the antinode for the open end of a pipe is located slightly beyond the end, but we shall not dwell on that detail.)
The simplest standing wave pattern that can be set up in a pipe with two open ends is shown in Fig. 17-14a. There is an antinode across each open end, as required. There is also a node across the middle of the pipe. An easier way of representing this standing longitudinal sound wave is shown in Fig. 17-14b—by drawing it as a standing transverse string wave.
The standing wave pattern of Fig. 17-14a is called the fundamental mode or first harmonic. For it to be set up, the sound waves in a pipe of length L must have a wavelength given by L = λ/2, so that λ = 2L. Several more standing sound wave patterns for a pipe with two open ends are shown in Fig. 17-15a using string wave representations. The second harmonic requires sound waves of wavelength λ = L, the third harmonic requires wavelength λ = 2L/3, and so on.
More generally, the resonant frequencies for a pipe of length L with two open ends correspond to the wavelengths
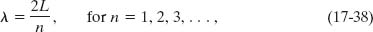
where n is called the harmonic number. The resonant frequencies for a pipe with two open ends are then given by

where ν is the speed of sound.
Figure 17-15b shows (using string wave representations) some of the standing sound wave patterns that can be set up in a pipe with only one open end. As required, across the open end there is an antinode and across the closed end there is a node. The simplest pattern requires sound waves having a wavelength given by L = λ /4, so that λ = 4L. The next simplest pattern requires a wavelength given by L = 3λ /4, so that λ = 4L/3, and so on.
More generally, the resonant frequencies for a pipe of length L with only one open end correspond to the wavelengths
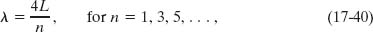
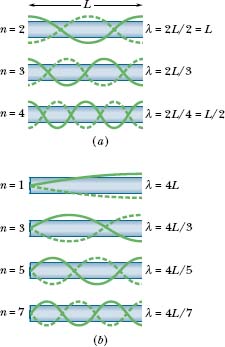
Fig. 17-15 Standing wave patterns for string waves superimposed on pipes to represent standing sound wave patterns in the pipes. (a) With both ends of the pipe open, any harmonic can be set up in the pipe. (b) With only one end open, only odd harmonics can be set up.
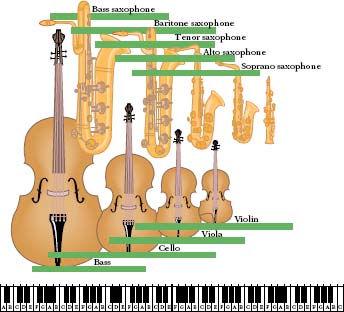
Fig. 17-16 The saxophone and violin families, showing the relations between instrument length and frequency range. The frequency range of each instrument is indicated by a horizontal bar along a frequency scale suggested by the keyboard at the bottom; the frequency increases toward the right.
in which the harmonic number n must be an odd number. The resonant frequencies are then given by
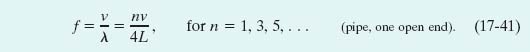
Note again that only odd harmonics can exist in a pipe with one open end. For example, the second harmonic, with n = 2, cannot be set up in such a pipe. Note also that for such a pipe the adjective in a phrase such as “the third harmonic” still refers to the harmonic number n (and not to, say, the third possible harmonic).
The length of a musical instrument reflects the range of frequencies over which the instrument is designed to function, and smaller length implies higher frequencies. Figure 17-16, for example, shows the saxophone and violin families, with their frequency ranges suggested by the piano keyboard. Note that, for every instrument, there is overlap with its higher- and lower-frequency neighbors.
In any oscillating system that gives rise to a musical sound, whether it is a violin string or the air in an organ pipe, the fundamental and one or more of the higher harmonics are usually generated simultaneously. Thus, you hear them together—that is, superimposed as a net wave. When different instruments are played at the same note, they produce the same fundamental frequency but different intensities for the higher harmonics. For example, the fourth harmonic of middle C might be relatively loud on one instrument and relatively quiet or even missing on another. Thus, because different instruments produce different net waves, they sound different to you even when they are played at the same note. That would be the case for the two net waves shown in Fig. 17-17, which were produced at the same note by different instruments.
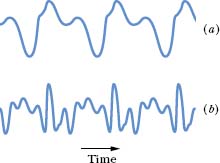
Fig. 17-17 The wave forms produced by (a) a flute and (b) an oboe when played at the same note, with the same first harmonic frequency.
![]() CHECKPOINT 4 Pipe A, with length L, and pipe B, with length 2L, both have two open ends. Which harmonic of pipe B has the same frequency as the fundamental of pipe A?
CHECKPOINT 4 Pipe A, with length L, and pipe B, with length 2L, both have two open ends. Which harmonic of pipe B has the same frequency as the fundamental of pipe A?
Weak background noises from a room set up the fundamental standing wave in a cardboard tube of length L = 67.0 cm with two open ends. Assume that the speed of sound in the air within the tube is 343 m/s.
(a) What frequency do you hear from the tube?
Solution: The Key Idea here is that, with both pipe ends open, we have a symmetric situation in which the standing wave has an antinode at each end of the tube. The standing wave pattern (in string wave style) is that of Fig. 17-14b. The frequency is given by Eq. 17-39 with n = 1 for the fundamental mode:
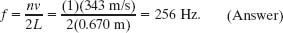
If the background noises set up any higher harmonics, such as the second harmonic, you also hear frequencies that are integer multiples of 256 Hz.
(b) If you jam your ear against one end of the tube, what fundamental frequency do you hear from the tube?
Solution: The Key Idea now is that, with your ear effectively closing one end of the tube, we have an asymmetric situation—an antinode still exists at the open end, but a node is now at the other (closed) end. The standing wave pattern is the top one in Fig. 17-15b. The frequency is given by Eq. 17-41 with n = 1 for the fundamental mode:
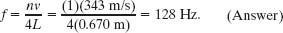
If the background noises set up any higher harmonics, they will be odd multiples of 128 Hz. That means that the frequency of 256 Hz (which is an even multiple) cannot now occur.
Leave a Reply