If we listen, a few minutes apart, to two sounds whose frequencies are, say, 552 and 564 Hz, most of us cannot tell one from the other. However, if the sounds reach our ears simultaneously, what we hear is a sound whose frequency is 558 Hz, the average of the two combining frequencies. We also hear a striking variation in the intensity of this sound—it increases and decreases in slow, wavering beats that repeat at a frequency of 12 Hz, the difference between the two combining frequencies. Figure 17-18 shows this beat phenomenon.
Let the time-dependent variations of the displacements due to two sound waves at a particular location be
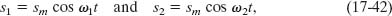
where ω1 > ω2. We have assumed, for simplicity, that the waves have the same amplitude. According to the superposition principle, the resultant displacement is
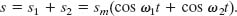
Using the trigonometric identity (see Appendix E)
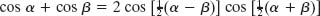
allows us to write the resultant displacement as
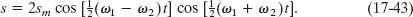
If we write
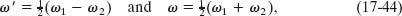
we can then write Eq. 17-43 as
We now assume that the angular frequencies ω1 and ω2 of the combining waves are almost equal, which means that ω 
ω′ in Eq. 17-44. We can then regard Eq. 17-45 as a cosine function whose angular frequency is ω and whose amplitude (which is not constant but varies with angular frequency ω′) is the absolute value of the quantity in the brackets.
Fig. 17-18 (a, b) The pressure variations Δp of two sound waves as they would be detected separately. The frequencies of the waves are nearly equal. (c) The resultant pressure variation if the two waves are detected simultaneously.
A maximum amplitude will occur whenever cos ω′t in Eq. 17-45 has the value +1 or −1, which happens twice in each repetition of the cosine function. Because cos ω′t has angular frequency ω′, the angular frequency ωbeat at which beats occur is ωbeat = 2ω′. Then, with the aid of Eq. 17-44, we can write
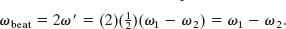
Because ω = 2πf, we can recast this as
Musicians use the beat phenomenon in tuning instruments. If an instrument is sounded against a standard frequency (for example, the note called “concert A” played on an orchestra’s first oboe) and tuned until the beat disappears, the instrument is in tune with that standard. In musical Vienna, concert A (440 Hz) is available as a telephone service for the city’s many musicians.
Most birds vocalize by using only one side of their two-sided vocal organ, called the syrinx. Emperor penguins, however, vocalize by using both sides simultaneously. Each side sets up acoustic standing waves in the bird’s throat and mouth, much like in a pipe with two open ends. Suppose that the frequency of the first harmonic produced by side A is fA1 = 432 Hz and the frequency of the first harmonic produced by side B is fB1 = 371 Hz. What is the beat frequency between those two first-harmonic frequencies and between the two second-harmonic frequencies?
Solution: The Key Idea here is that the beat frequency between two frequencies is their difference, as given by Eq. 17-46 (fbeat = f1 − f2). For the two first-harmonic frequencies fA1 and fB1, the beat frequency is
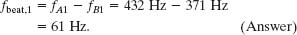
Because the standing waves in the penguin are effectively in a pipe with two open ends, the resonant frequencies are given by Eq. 17-39 (f = nv/2L), in which L is the (unknown) length of the effective pipe. The first-harmonic frequency is f1 = ν/2L, and the second-harmonic frequency is f2 = 2ν/2L. Comparing these two frequencies, we see that, in general,
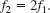
For the penguin, the second harmonic of side A has frequency fA2 = 2fA1 and the second harmonic of side B has frequency fB2 = 2fB1. Using Eq. 17-46 with frequencies fA2 and fB2, we find that the corresponding beat frequency is
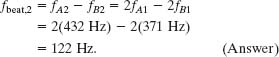
Experiments indicate that penguins can perceive such large beat frequencies (humans cannot). Thus, a penguin’s cry can be rich with different harmonics and different beat frequencies, allowing the voice to be recognized even among the voices of thousands of other, closely huddled penguins.
Leave a Reply