The speed of a wave is related to the wave’s wavelength and frequency by Eq. 16-13, but it is set by the properties of the medium. If a wave is to travel through a medium such as water, air, steel, or a stretched string, it must cause the particles of that medium to oscillate as it passes. For that to happen, the medium must possess both mass (so that there can be kinetic energy) and elasticity (so that there can be potential energy). Thus, the medium’s mass and elasticity properties determine how fast the wave can travel in the medium. Conversely, it should be possible to calculate the speed of the wave through the medium in terms of these properties. We do so now for a stretched string, in two ways.
Dimensional Analysis
In dimensional analysis we carefully examine the dimensions of all the physical quantities that enter into a given situation to determine the quantities they produce. In this case, we examine mass and elasticity to find a speed v, which has the dimension of length divided by time, or LT−1.
For the mass, we use the mass of a string element, which is represented by the mass m of the string divided by the length l of the string. We call this ratio the linear density μ of the string. Thus, μ = m/l, its dimension being mass divided by length, ML−1.
You cannot send a wave along a string unless the string is under tension, which means that it has been stretched and pulled taut by forces at its two ends. The tension τ in the string is equal to the common magnitude of those two forces. As a wave travels along the string, it displaces elements of the string by causing additional stretching, with adjacent sections of string pulling on each other because of the tension. Thus, we can associate the tension in the string with the stretching (elasticity) of the string. The tension and the stretching forces it produces have the dimension of a force—namely, MLT−2 (from F = ma).
The goal here is to combine μ (dimension ML−1) and τ (dimension MLT−2) in such a way as to generate v (dimension LT−1). A little juggling of various combinations suggests
in which C is a dimensionless constant that cannot be determined with dimensional analysis. In our second approach to determining wave speed, you will see that Eq. 16-22 is indeed correct and that C = 1.
Derivation from Newton’s Second Law
Instead of the sinusoidal wave of Fig. 16-1b, let us consider a single symmetrical pulse such as that of Fig. 16-10, moving from left to right along a string with speed v. For convenience, we choose a reference frame in which the pulse remains stationary; that is, we run along with the pulse, keeping it constantly in view. In this frame, the string appears to move past us, from right to left in Fig. 16-10, with speed v.
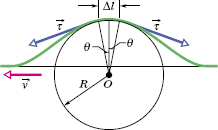
Fig. 16-10 A symmetrical pulse, viewed from a reference frame in which the pulse is stationary and the string appears to move right to left with speed v. We find speed v by applying Newton’s second law to a string element of length Δl, located at the top of the pulse.
Consider a small string element of length Δl within the pulse, an element that forms an arc of a circle of radius R and subtending an angle 2θ at the center of that circle. A force 
with a magnitude equal to the tension in the string pulls tangentially on this element at each end. The horizontal components of these forces cancel, but the vertical components add to form a radial restoring force 
. In magnitude,
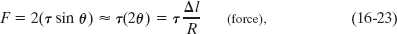
where we have approximated sin θ as θ for the small angles θ in Fig. 16-10. From that figure, we have also used 2θ = Δl/R.
The mass of the element is given by
where μ is the string’s linear density.
At the moment shown in Fig. 16-10, the string element Δl is moving in an arc of a circle. Thus, it has a centripetal acceleration toward the center of that circle, given by
Equations 16-23, 16-24, and 16-25 contain the elements of Newton’s second law. Combining them in the form
force = mass × acceleration
gives
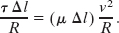
Solving this equation for the speed v yields
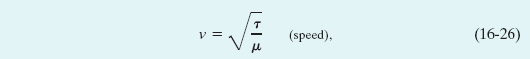
in exact agreement with Eq. 16-22 if the constant C in that equation is given the value unity. Equation 16-26 gives the speed of the pulse in Fig. 16-10 and the speed of any other wave on the same string under the same tension.
Equation 16-26 tells us:
The speed of a wave along a stretched ideal string depends only on the tension and linear density of the string and not on the frequency of the wave.
The frequency of the wave is fixed entirely by whatever generates the wave (for example, the person in Fig. 16-1b). The wavelength of the wave is then fixed by Eq. 16-13 in the form λ = v/f.
CHECK POINT 3 You send a traveling wave along a particular string by oscillating one end. If you increase the frequency of the oscillations, do (a) the speed of the wave and (b) the wavelength of the wave increase, decrease, or remain the same? If, instead, you increase the tension in the string, do (c) the speed of the wave and (d) the wavelength of the wave increase, decrease, or remain the same?
In Fig. 16-11, two strings have been tied together with a knot and then stretched between two rigid supports. The strings have linear densities μ1 = 1.4 × 10−4 kg/m and μ2 = 2.8 × 10−4 kg/m. Their lengths are L1 = 3.0 m and L2 = 2.0 m, and string 1 is under a tension of 400 N. Simultaneously, on each string a pulse is sent from the rigid support end, toward the knot. Which pulse reaches the knot first?
Solution: We need several Key Ideas here:
1. The time t taken by a pulse to travel a length L is t = L/v, where v is the constant speed of the pulse.
2. The speed of a pulse on a stretched string depends on the string’s tension τ and linear density μ, and is given by Eq. 16-26 
.
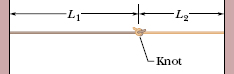
Fig. 16-11 Two strings, of lengths L1 and L2, tied together with a knot and stretched between two rigid supports.
3. Because the two strings are stretched together, they must both be under the same tension τ (= 400 N).
Putting these three ideas together gives us, as the time for the pulse on string 1 to reach the knot,
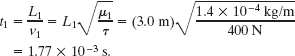
Similarly, the data for the pulse on string 2 give us
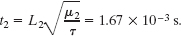
Thus, the pulse on string 2 reaches the knot first.
Now look back at Key Idea 2. The linear density of string 2 is greater than that of string 1, so the pulse on string 2 must be slower than that on string 1. Could we have guessed the answer from that fact alone? No, because from the first Key Idea we see that the distance traveled by a pulse also matters.
Leave a Reply