Suppose we send two sinusoidal waves of the same wavelength and amplitude in the same direction along a stretched string. The superposition principle applies. What resultant wave does it predict for the string?
The resultant wave depends on the extent to which the waves are in phase (in step) with respect to each other—that is, how much one wave form is shifted from the other wave form. If the waves are exactly in phase (so that the peaks and valleys of one are exactly aligned with those of the other), they combine to double the displacement of either wave acting alone. If they are exactly out of phase (the peaks of one are exactly aligned with the valleys of the other), they combine to cancel everywhere, and the string remains straight. We call this phenomenon of combining waves interference, and the waves are said to interfere. (These terms refer only to the wave displacements; the travel of the waves is unaffected.)
Let one wave traveling along a stretched string be given by
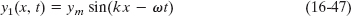
and another, shifted from the first, by
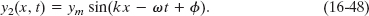
These waves have the same angular frequency ω (and thus the same frequency f ), the same angular wave number k (and thus the same wavelength λ), and the same amplitude y . They both travel in the positive direction of the x axis, with the same speed, given by Eq. 16-26. They differ only by a constant angle ![]() , the phase constant. These waves are said to be out of phase by
, the phase constant. These waves are said to be out of phase by ![]() or to have a phase difference of
or to have a phase difference of ![]() , or one wave is said to be phase-shifted from the other by
, or one wave is said to be phase-shifted from the other by ![]() .
.
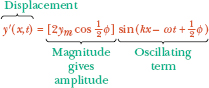
Fig. 16-15 The resultant wave of Eq. 16-51, due to the interference of two sinusoidal transverse waves, is also a sinusoidal transverse wave, with an amplitude and an oscillating term.
From the principle of superposition (Eq. 16-46), the resultant wave is the algebraic sum of the two interfering waves and has displacement
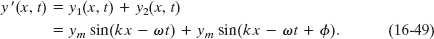
In Appendix E we see that we can write the sum of the sines of two angles α and β as
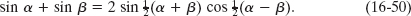
Applying this relation to Eq. 16-49 leads to
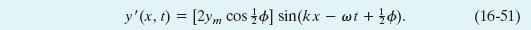
As Fig. 16-15 shows, the resultant wave is also a sinusoidal wave traveling in the direction of increasing x. It is the only wave you would actually see on the string (you would not see the two interfering waves of Eqs. 16-47 and 16-48).
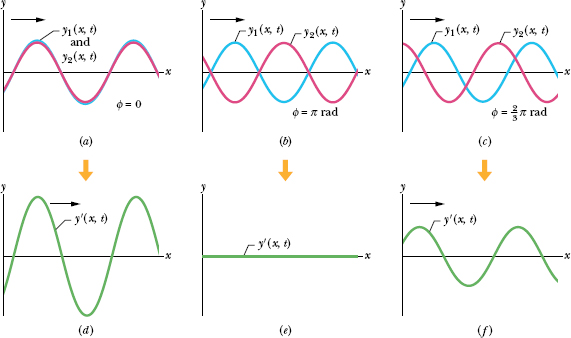
Fig. 16-16 Two identical sinusoidal waves, y1(x, t) and y2(x, t), travel along a string in the positive direction of an x axis. They interfere to give a resultant wave y′(x, t). The resultant wave is what is actually seen on the string. The phase difference ![]() between the two interfering waves is (a) 0 rad or 0º, (b) π rad or 180º, and (c)
between the two interfering waves is (a) 0 rad or 0º, (b) π rad or 180º, and (c) ![]() π rad or 120º. The corresponding resultant waves are shown in (d), (e), and (f).
π rad or 120º. The corresponding resultant waves are shown in (d), (e), and (f).
![]() If two sinusoidal waves of the same amplitude and wavelength travel in the same direction along a stretched string, they interfere to produce a resultant sinusoidal wave traveling in that direction.
If two sinusoidal waves of the same amplitude and wavelength travel in the same direction along a stretched string, they interfere to produce a resultant sinusoidal wave traveling in that direction.
The resultant wave differs from the interfering waves in two respects: (1) its phase constant is ![]() , and (2) its amplitude
, and (2) its amplitude ![]() is the magnitude of the quantity in the brackets in Eq. 16-51:
is the magnitude of the quantity in the brackets in Eq. 16-51:
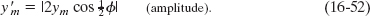
If ![]() = 0 rad (or 0º), the two interfering waves are exactly in phase, as in Fig. 16-16a. Then Eq. 16-51 reduces to
= 0 rad (or 0º), the two interfering waves are exactly in phase, as in Fig. 16-16a. Then Eq. 16-51 reduces to

This resultant wave is plotted in Fig. 16-16d. Note from both that figure and Eq. 16-53 that the amplitude of the resultant wave is twice the amplitude of either interfering wave. That is the greatest amplitude the resultant wave can have, because the cosine term in Eqs. 16-51 and 16-52 has its greatest value (unity) when ![]() = 0. Interference that produces the greatest possible amplitude is called fully constructive interference.
= 0. Interference that produces the greatest possible amplitude is called fully constructive interference.
If ![]() = π rad (or 180º), the interfering waves are exactly out of phase as in Fig. 16-16b. Then cos
= π rad (or 180º), the interfering waves are exactly out of phase as in Fig. 16-16b. Then cos ![]() becomes cos π/2 = 0, and the amplitude of the resultant wave as given by Eq. 16-52 is zero. We then have, for all values of x and t,
becomes cos π/2 = 0, and the amplitude of the resultant wave as given by Eq. 16-52 is zero. We then have, for all values of x and t,
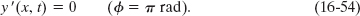
The resultant wave is plotted in Fig. 16-16e. Although we sent two waves along the string, we see no motion of the string. This type of interference is called fully destructive interference.
Because a sinusoidal wave repeats its shape every 2π rad, a phase difference ![]() = 2π rad (or 360º) corresponds to a shift of one wave relative to the other wave by a distance equivalent to one wavelength. Thus, phase differences can be described in terms of wavelengths as well as angles. For example, in Fig. 16-16b the waves may be said to be 0.50 wavelength out of phase. Table 16-1 shows some other examples of phase differences and the interference they produce. Note that when interference is neither fully constructive nor fully destructive, it is called intermediate interference. The amplitude of the resultant wave is then intermediate between 0 and 2ym. For example, from Table 16-1, if the interfering waves have a phase difference of 120º (
= 2π rad (or 360º) corresponds to a shift of one wave relative to the other wave by a distance equivalent to one wavelength. Thus, phase differences can be described in terms of wavelengths as well as angles. For example, in Fig. 16-16b the waves may be said to be 0.50 wavelength out of phase. Table 16-1 shows some other examples of phase differences and the interference they produce. Note that when interference is neither fully constructive nor fully destructive, it is called intermediate interference. The amplitude of the resultant wave is then intermediate between 0 and 2ym. For example, from Table 16-1, if the interfering waves have a phase difference of 120º (![]() wavelength), then the resultant wave has an amplitude of ym, the same as that of the interfering waves (see Figs. 16-16c and f).
wavelength), then the resultant wave has an amplitude of ym, the same as that of the interfering waves (see Figs. 16-16c and f).

Two waves with the same wavelength are in phase if their phase difference is zero or any integer number of wavelengths. Thus, the integer part of any phase difference expressed in wavelengths may be discarded. For example, a phase difference of 0.40 wavelength is equivalent in every way to one of 2.40 wavelengths, and so the simpler of the two numbers can be used in computations.
Two identical sinusoidal waves, moving in the same direction along a stretched string, interfere with each other. The amplitude ym of each wave is 9.8 mm, and the phase difference ![]() between them is 100º.
between them is 100º.
(a) What is the amplitude ![]() of the resultant wave due to the interference, and what is the type of this interference?
of the resultant wave due to the interference, and what is the type of this interference?
Solution: The Key Idea here is that these are identical sinusoidal waves traveling in the same direction along a string, so they interfere to produce a sinusoidal traveling wave. Because they are identical, they have the same amplitude. Thus, the amplitude ![]() of the resultant wave is given by Eq. 16-52:
of the resultant wave is given by Eq. 16-52:
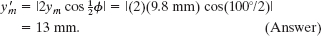
We can tell that the interference is intermediate in two ways. The phase difference is between 0 and 180º, and, correspondingly, the amplitude ![]() is between 0 and 2ym (= 19.6 mm).
is between 0 and 2ym (= 19.6 mm).
(b) What phase difference, in radians and wavelengths, will give the resultant wave an amplitude of 4.9 mm?
Solution: The same Key Idea applies here as in part (a), but
now we are given ![]() and
and ![]() . From Eq. 16-52,
. From Eq. 16-52,
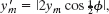
we now have
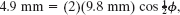
which gives us (with a calculator in the radian mode)
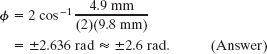
There are two solutions because we can obtain the same resultant wave by letting the first wave lead (travel ahead of) or lag (travel behind) the second wave by 2.6 rad. In wavelengths, the phase difference is
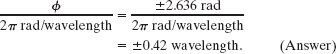
![]() CHECK POINT 5 Here are four other possible phase differences between the two waves of this sample problem, expressed in wavelengths: 0.20, 0.45, 0.60, and 0.80. Rank them according to the amplitude of the resultant wave, greatest first.
CHECK POINT 5 Here are four other possible phase differences between the two waves of this sample problem, expressed in wavelengths: 0.20, 0.45, 0.60, and 0.80. Rank them according to the amplitude of the resultant wave, greatest first.
Leave a Reply