Energy and Power of a Wave Traveling Along a String

When we set up a wave on a stretched string, we provide energy for the motion of the string. As the wave moves away from us, it transports that energy as both kinetic energy and elastic potential energy. Let us consider each form in turn.

Kinetic Energy

A string element of mass dm, oscillating transversely in simple harmonic motion as the wave passes through it, has kinetic energy associated with its transverse velocity . When the element is rushing through its y = 0 position (element b in Fig. 16-12), its transverse velocity—and thus its kinetic energy—is a maximum. When the element is at its extreme position y = y_m (as is element a), its transverse velocity—and thus its kinetic energy—is zero.

Elastic Potential Energy

To send a sinusoidal wave along a previously straight string, the wave must necessarily stretch the string. As a string element of length dx oscillates transversely, its length must increase and decrease in a periodic way if the string element is to fit the sinusoidal wave form. Elastic potential energy is associated with these length changes, just as for a spring.

When the string element is at its y = y_m position (element a in Fig. 16-12), its length has its normal undisturbed value dx, so its elastic potential energy is zero. However, when the element is rushing through its y = 0 position, it has maximum stretch and thus maximum elastic potential energy.

Energy Transport

The oscillating string element thus has both its maximum kinetic energy and its maximum elastic potential energy at y = 0. In the snapshot of Fig. 16-12, the regions of the string at maximum displacement have no energy, and the regions at zero displacement have maximum energy. As the wave travels along the string, forces due to the tension in the string continuously do work to transfer energy from regions with energy to regions with no energy.

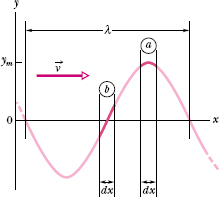
Fig. 16-12   A snapshot of a traveling wave on a string at time t = 0. String element a is at displacement y = y_m, and string element b is at displacement y = 0. The kinetic energy of the string element at each position depends on the transverse velocity of the element. The potential energy depends on the amount by which the string element is stretched as the wave passes through it.

Suppose we set up a wave on a string stretched along a horizontal x axis so that Eq. 16-2 describes the string’s displacement. We might send a wave along the string by continuously oscillating one end of the string, as in Fig. 16-1b. In doing so, we continuously provide energy for the motion and stretching of the string—as the string sections oscillate perpendicularly to the x axis, they have kinetic energy and elastic potential energy. As the wave moves into sections that were previously at rest, energy is transferred into those new sections. Thus, we say that the wave transports the energy along the string.

The Rate of Energy Transmission

The kinetic energy dK associated with a string element of mass dm is given by

where u is the transverse speed of the oscillating string element. To find u, we differentiate Eq. 16-2 with respect to time while holding x constant:

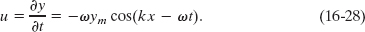
Using this relation and putting dm = μ dx, we rewrite Eq. 16-27 as

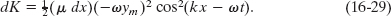
Dividing Eq. 16-29 by dt gives the rate at which kinetic energy passes through a string element, and thus the rate at which kinetic energy is carried along by the wave. The ratio dx/dt that then appears on the right of Eq. 16-29 is the wave speed v, so we obtain

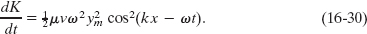
The average rate at which kinetic energy is transported is

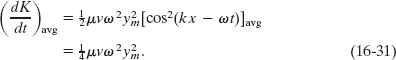
Here we have taken the average over an integer number of wavelengths and have used the fact that the average value of the square of a cosine function over an integer number of periods is .

Elastic potential energy is also carried along with the wave, and at the same average rate given by Eq. 16-31. Although we shall not examine the proof, you should recall that, in an oscillating system such as a pendulum or a spring–block system, the average kinetic energy and the average potential energy are equal.

The average power, which is the average rate at which energy of both kinds is transmitted by the wave, is then

or, from Eq. 16-31,

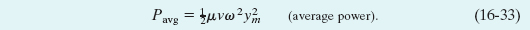
The factors μ and v in this equation depend on the material and tension of the string. The factors ω and y_m depend on the process that generates the wave. The dependence of the average power of a wave on the square of its amplitude and also on the square of its angular frequency is a general result, true for waves of all types.

Sample Problem 16-5

A stretched string has linear density μ = 525 g/m and is under tension τ = 45 N. We send a sinusoidal wave with frequency f = 120 Hz and amplitude y_m = 8.5 mm along the string. At what average rate does the wave transport energy?

Solution: The Key Idea here is that the average rate of energy transport is the average power P_avg as given by Eq. 16-33. To use that equation, however, we first must calculate angular frequency ω and wave speed v. From Eq. 16-9,

ω = 2πf = (2π)(120 Hz) = 754 rad/s.

From Eq. 16-26 we have

Equation 16-33 then yields

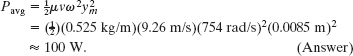
 CHECK POINT 4 For the string and wave of this sample problem, we can adjust three parameters: the tension in the string, the frequency of the wave, and the amplitude of the wave. Does the average rate at which the wave transports energy along the string increase, decrease, or remain the same if we increase (a) the tension, (b) the frequency, and (c) the amplitude?