Once we know how the acceleration of a particle varies with time, we can use Newton’s second law to learn what force must act on the particle to give it that acceleration. If we combine Newton’s second law and Eq. 15-8, we find, for simple harmonic motion,
This result—a restoring force that is proportional to the displacement but opposite in sign—is familiar. It is Hooke’s law,
for a spring, the spring constant here being
We can in fact take Eq. 15-10 as an alternative definition of simple harmonic motion. It says:
Simple harmonic motion is the motion executed by a particle subject to a force that is proportional to the displacement of the particle but opposite in sign.
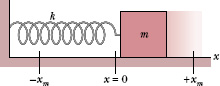
Fig. 15-5 A linear simple harmonic oscillator. The surface is frictionless. Like the particle of Fig. 15-1, the block moves in simple harmonic motion once it has been either pulled or pushed away from the x = 0 position and released. Its displacement is then given by Eq. 15-3.
The block–spring system of Fig. 15-5 forms a linear simple harmonic oscillator (linear oscillator, for short), where “linear” indicates that F is proportional to x rather than to some other power of x. The angular frequency ω of the simple harmonic motion of the block is related to the spring constant k and the mass m of the block by Eq. 15-11, which yields
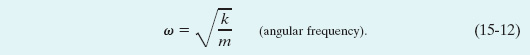
By combining Eqs. 15-5 and 15-12, we can write, for the period of the linear oscillator of Fig. 15-5,
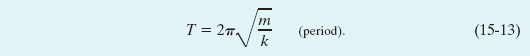
Equations 15-12 and 15-13 tell us that a large angular frequency (and thus a small period) goes with a stiff spring (large k) and a light block (small m).
Every oscillating system, be it a diving board or a violin string, has some element of “springiness” and some element of “inertia” or mass, and thus resembles a linear oscillator. In the linear oscillator of Fig. 15-5, these elements are located in separate parts of the system: The springiness is entirely in the spring, which we assume to be massless, and the inertia is entirely in the block, which we assume to be rigid. In a violin string, however, the two elements are both within the string, as you will see in Lesson 16.
CHECKPOINT 2 Which of the following relationships between the force F on a particle and the particle’s position x implies simple harmonic oscillation: (a) F = −5x, (b) F = −400x2, (c) F = 10x, (d) F = 3x2?
A block whose mass m is 680 g is fastened to a spring whose spring constant k is 65 N/m. The block is pulled a distance x = 11 cm from its equilibrium position at x = 0 on a frictionless surface and released from rest at t = 0.
(a) What are the angular frequency, the frequency, and the period of the resulting motion?
Solution: The Key Idea here is that the block–spring system forms a linear simple harmonic oscillator, with the block undergoing SHM. Then the angular frequency is given by Eq. 15-12:
The frequency follows from Eq. 15-5, which yields
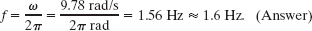
The period follows from Eq. 15-2, which yields
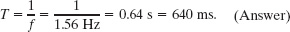
(b) What is the amplitude of the oscillation?
Solution: The Key Idea here is that, with no friction involved, the mechanical energy of the spring–block system is conserved. The block is released from rest 11 cm from its equilibrium position, with zero kinetic energy and the elastic potential energy of the system at a maximum. Thus, the block will have zero kinetic energy whenever it is again 11 cm from its equilibrium position, which means it will never be farther than 11 cm from that position. Its maximum displacement is 11 cm:
xm = 11 cm. (Answer)
(c) What is the maximum speed vm of the oscillating block, and where is the block when it has this speed?
Solution: The Key Idea here is that the maximum speed vm is the velocity amplitude ωxm in Eq. 15-6; that is,
vm = ωxm = (9.78 rad/s)(0.11 m)
= 1.1 m/s. (Answer)
This maximum speed occurs when the oscillating block is rushing through the origin; compare Figs. 15-4a and 15-4b, where you can see that the speed is a maximum whenever x = 0.
(d) What is the magnitude am of the maximum acceleration of the block?
Solution: The Key Idea this time is that the magnitude am of the maximum acceleration is the acceleration amplitude ω2xm in Eq. 15-7; that is,
am = ω2xm = (9.78 rad/s)2(0.11 m)
= 11 m/s2. (Answer)
This maximum acceleration occurs when the block is at the ends of its path. At those points, the force acting on the block has its maximum magnitude; compare Figs. 15-4a and 15-4c, where you can see that the magnitudes of the displacement and acceleration are maximum at the same times.
(e) What is the phase constant 
for the motion?
Solution: Here the Key Idea is that Eq. 15-3 gives the displacement of the block as a function of time. We know that at time t = 0, the block is located at x = xm. Substituting these initial conditions, as they are called, into Eq. 15-3 and canceling xm give us
Taking the inverse cosine then yields
(Any angle that is an integer multiple of 2π rad also satisfies Eq. 15-14; we chose the smallest angle.)
(f) What is the displacement function x(t) for the spring–block system?
Solution: The Key Idea here is that x(t) is given in general form by Eq. 15-3. Substituting known quantities into that equation gives us
x(t) = xm cos(ωt + )
= (0.11 m) cos[(9.8 rad/s)t + 0]
= 0.11 cos(9.8t), (Answer)
where x is in meters and t is in seconds.
At t = 0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15-5 is −8.50 cm. (Read x(0) as “x at time zero.”) The block’s velocity v(0) then is −0.920 m/s, and its acceleration a(0) is +47.0 m/s2.
(a) What is the angular frequency ω of this system?
Solution: A Key Idea here is that, with the block in SHM, Eqs. 15-3, 15-6, and 15-7 give its displacement, velocity, and acceleration, respectively, and each contains ω. Let’s substitute t = 0 into each to see whether we can solve any one of them for ω. We find
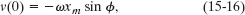
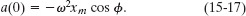
and
In Eq. 15-15, ω has disappeared. In Eqs. 15-16 and 15-17, we know values for the left sides, but we do not know xm and . However, if we divide Eq. 15-17 by Eq. 15-15, we neatly eliminate both xm and and can then solve for ω as
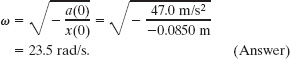
(b) What are the phase constant and amplitude xm?
Solution: The same Key Idea as in part (a) also applies here, as do Eqs. 15-15 through 15-17. Now, however, we know ω and want and xm. If we divide Eq. 15-16 by Eq. 15-15, we find
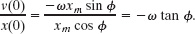
Solving for tan , we find
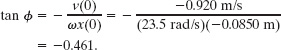
This equation has two solutions:
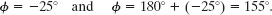
(Normally only the first solution here is displayed by a calculator.) A Key Idea in choosing the proper solution is to test them both by using them to compute values for the amplitude xm. From Eq. 15-15, we find that if 
, then
We find similarly that if 
, then xm = 0.094 m. Because the amplitude of SHM must be a positive constant, the correct phase constant and amplitude here are
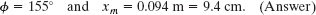
PROBLEM – SOLVING TACTICS
TACTIC 2: Identifying SHM
In linear SHM the acceleration a and displacement x of the system are related by an equation of the form
a = −(a positive constant)x,
which says that the acceleration is proportional to the displacement from the equilibrium position but is in the opposite direction. Once you find such an expression for an oscillating system, you can immediately compare it with Eq. 15-8, identify the positive constant as being equal to ω2, and so quickly get an expression for the angular frequency of the motion. With Eq. 15-5 you then can find the period T and the frequency f.
In some problems you might derive an expression for the force F as a function of displacement x. If the motion is linear SHM, the force and displacement are related by
F = −(a positive constant)x,
which says that the force is proportional to the displacement but is in the opposite direction. Once you have found such an expression, you can immediately compare it with Eq. 15-10 and identify the positive constant as being k. If you know the mass that is involved, you can then use Eqs. 15-12, 15-13, and 15-5 to find the angular frequency ω, period T, and frequency f.
Leave a Reply