In 1610, Galileo, using his newly constructed telescope, discovered the four principal moons of Jupiter. Over weeks of observation, each moon seemed to him to be moving back and forth relative to the planet in what today we would call simple harmonic motion; the disk of the planet was the midpoint of the motion. The record of Galileo’s observations, written in his own hand, is still available. A. P. French of MIT used Galileo’s data to work out the position of the moon Callisto relative to Jupiter. In the results shown in Fig. 15-13, the circles are based on Galileo’s observations and the curve is a best fit to the data. The curve strongly suggests Eq. 15-3, the displacement function for SHM. A period of about 16.8 days can be measured from the plot.
Actually, Callisto moves with essentially constant speed in an essentially circular orbit around Jupiter. Its true motion—far from being simple harmonic—is uniform circular motion. What Galileo saw—and what you can see with a good pair of binoculars and a little patience—is the projection of this uniform circular motion on a line in the plane of the motion. We are led by Galileo’s remarkable observations to the conclusion that simple harmonic motion is uniform circular motion viewed edge-on. In more formal language:
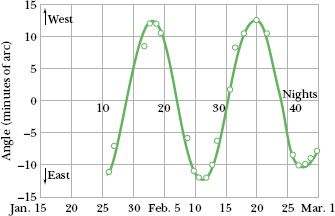
Fig. 15-13 The angle between Jupiter and its moon Callisto as seen from Earth. The circles are based on Galileo’s 1610 measurements. The curve is a best fit, strongly suggesting simple harmonic motion. At Jupiter’s mean distance from Earth, 10 minutes of arc corresponds to about 2 × 106 km. (Adapted from A. P. French, Newtonian Mechanics, W. W. Norton & Company, New York, 1971, p. 288.)
Simple harmonic motion is the projection of uniform circular motion on a diameter of the circle in which the circular motion occurs.
Figure 15-14a gives an example. It shows a reference particle P′ moving in uniform circular motion with (constant) angular speed ω in a reference circle. The radius xm of the circle is the magnitude of the particle’s position vector. At any time t, the angular position of the particle is ωt + 
, where is its angular position at t = 0.
The projection of particle P′ onto the x axis is a point P, which we take to be a second particle. The projection of the position vector of particle P ′ onto the x axis gives the location x(t) of P. Thus, we find
x(t) = xm cos(ωt + ),
which is precisely Eq. 15-3. Our conclusion is correct. If reference particle P′ moves in uniform circular motion, its projection particle P moves in simple harmonic motion along a diameter of the circle.
Figure 15-14b shows the velocity 
of the reference particle. From Eq. 10-18 (v = ωr), the magnitude of the velocity vector is ωxm; its projection on the x axis is
v(t) = −ωxm sin(ωt + ),
Fig. 15-14 (a) A reference particle P′ moving with uniform circular motion in a reference circle of radius xm. Its projection P on the x axis executes simple harmonic motion. (b) The projection of the velocity 
of the reference particle is the velocity of SHM. (c) The projection of the radial acceleration 
of the reference particle is the acceleration of SHM.
which is exactly Eq. 15-6. The minus sign appears because the velocity component of P in Fig. 15-14b is directed to the left, in the negative direction of x.
Figure 15-14c shows the radial acceleration 
of the reference particle. From Eq. 10-23 (ar = ω2r), the magnitude of the radial acceleration vector is ω2xm; its projection on the x axis is
a(t) = −ω2xm cos(ωt + ),
which is exactly Eq. 15-7. Thus, whether we look at the displacement, the velocity, or the acceleration, the projection of uniform circular motion is indeed simple harmonic motion.
Leave a Reply