Forced Oscillations and Resonance

A person swinging in a swing without anyone pushing it is an example of free oscillation. However, if someone pushes the swing periodically, the swing has forced, or driven, oscillations. Two angular frequencies are associated with a system undergoing driven oscillations: (1) the natural angular frequency ω of the system, which is the angular frequency at which it would oscillate if it were suddenly disturbed and then left to oscillate freely, and (2) the angular frequency ω_d of the external driving force causing the driven oscillations.

We can use Fig. 15-15 to represent an idealized forced simple harmonic oscillator if we allow the structure marked “rigid support” to move up and down at a variable angular frequency ω_d. Such a forced oscillator oscillates at the angular frequency ω_d of the driving force, and its displacement x(t) is given by

where x_m is the amplitude of the oscillations.

How large the displacement amplitude x_m is depends on a complicated function of ω_d and ω. The velocity amplitude v_m of the oscillations is easier to describe: it is greatest when

a condition called resonance. Equation 15-46 is also approximately the condition at which the displacement amplitude x_m of the oscillations is greatest. Thus, if you push a swing at its natural angular frequency, the displacement and velocity amplitudes will increase to large values, a fact that children learn quickly by trial and error. If you push at other angular frequencies, either higher or lower, the displacement and velocity amplitudes will be smaller.

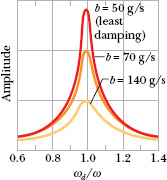
Fig. 15-17   The displacement amplitude x_m of a forced oscillator varies as the angular frequency ω_d of the driving force is varied. The curves here correspond to three values of the damping constant b.

Figure 15-17 shows how the displacement amplitude of an oscillator depends on the angular frequency ω_d of the driving force, for three values of the damping coefficient b. Note that for all three the amplitude is approximately greatest when ω_d/ω = 1 (the resonance condition of Eq. 15-46). The curves of Fig. 15-17 show that less damping gives a taller and narrower resonance peak.

All mechanical structures have one or more natural angular frequencies, and if a structure is subjected to a strong external driving force that matches one of these angular frequencies, the resulting oscillations of the structure may rupture it. Thus, for example, aircraft designers must make sure that none of the natural angular frequencies at which a wing can oscillate matches the angular frequency of the engines in flight. A wing that flaps violently at certain engine speeds would obviously be dangerous.

Resonance appears to be one reason buildings in Mexico City collapsed in September 1985 when a major earthquake (8.1 on the Richter scale) occurred on the western coast of Mexico. The seismic waves from the earthquake should have been too weak to cause extensive damage when they reached Mexico City about 400 km away. However, Mexico City is largely built on an ancient lake bed, where the soil is still soft with water. Although the amplitude of the seismic waves was small in the firmer ground en route to Mexico City, their amplitude substantially increased in the loose soil of the city. Acceleration amplitudes of the waves were as much as 0.20g, and the angular frequency was (surprisingly) concentrated around 3 rad/s. Not only was the ground severely oscillated, but many intermediate-height buildings had resonant angular frequencies of about 3 rad/s. Most of those buildings collapsed during the shaking (Fig. 15-18), while shorter buildings (with higher resonant angular frequencies) and taller buildings (with lower resonant angular frequencies) remained standing.

Fig. 15-18   In 1985, buildings of intermediate height collapsed in Mexico City as a result of an earthquake far from the city. Taller and shorter buildings remained standing.