Energy in Simple Harmonic Motion

In Lesson 8 we saw that the energy of a linear oscillator transfers back and forth between kinetic energy and potential energy, while the sum of the two—the mechanical energy E of the oscillator—remains constant. We now consider this situation quantitatively.

The potential energy of a linear oscillator like that of Fig. 15-5 is associated entirely with the spring. Its value depends on how much the spring is stretched or compressed—that is, on x(t). We can use Eqs. 8-11 and 15-3 to find

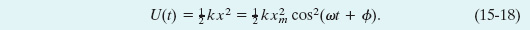
Caution: A function written in the form cos² A (as here) means (cos A)² and is not the same as one written cos A², which means cos (A²).

The kinetic energy of the system of Fig. 15-5 is associated entirely with the block. Its value depends on how fast the block is moving—that is, on v(t). We can use Eq. 15-6 to find

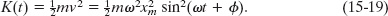
If we use Eq. 15-12 to substitute k/m for ω², we can write Eq. 15-19 as

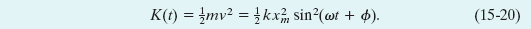
The mechanical energy follows from Eqs. 15-18 and 15-20 and is

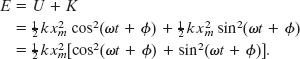
For any angle α,

cos² α + sin² α = 1.

Thus, the quantity in the square brackets above is unity and we have

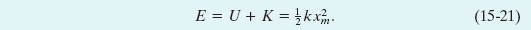
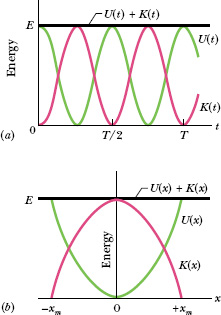
Fig. 15-6   (a) Potential energy U(t), kinetic energy K(t), and mechanical energy E as functions of time t for a linear harmonic oscillator. Note that all energies are positive and that the potential energy and the kinetic energy peak twice during every period. (b) Potential energy U(x), kinetic energy K(x), and mechanical energy E as functions of position x for a linear harmonic oscillator with amplitude x_m. For x = 0 the energy is all kinetic, and for x = ±x_m it is all potential.

The mechanical energy of a linear oscillator is indeed constant and independent of time. The potential energy and kinetic energy of a linear oscillator are shown as functions of time t in Fig. 15-6a, and they are shown as functions of displacement x in Fig. 15-6b.

You might now understand why an oscillating system normally contains an element of springiness and an element of inertia: The former stores its potential energy and the latter stores its kinetic energy.

CHECKPOINT 3    In Fig. 15-5, the block has a kinetic energy of 3 J and the spring has an elastic potential energy of 2 J when the block is at x = +2.0 cm. (a) What is the kinetic energy when the block is at x = 0? What is the elastic potential energy when the block is at (b) x = −2.0 cm and (c) x = −x_m?

Sample Problem 15-3

(a) What is the mechanical energy E of the linear oscillator of Sample Problem 15-1? (Initially, the block’s position is x = 11 cm and its speed is v = 0. Spring constant k is 65 N/m.)

Solution: The Key Idea here is that the mechanical energy E (the sum of the kinetic energy  of the block and the potential energy  of the spring) is constant throughout the motion of the oscillator. Thus, we can evaluate E at any point during the motion. Because we are given the initial conditions of the oscillator as x = 11 cm and v = 0, let us evaluate E for those conditions. We find

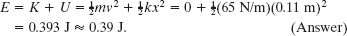
(b) What are the potential energy U and kinetic energy K of the oscillator when the block is at ? What are they when the block is at ?

Solution: The Key Idea here is that, because we are given the location of the block, we can easily find the spring’s potential energy with . For , we have

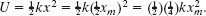
We can substitute for k and x_m, or we can use the Key Idea that the total mechanical energy, which we know from part (a), is . That idea allows us to write, from the above equation,

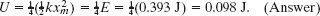
Now, using again the Key Idea that E = K + U, we can write

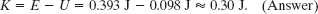
By repeating these calculations for , we would find the same answers for that displacement, consistent with the left–right symmetry of Fig. 15-6b.