Figure 15-7 shows an angular version of a simple harmonic oscillator; the element of springiness or elasticity is associated with the twisting of a suspension wire rather than the extension and compression of a spring as we previously had. The device is called a torsion pendulum, with torsion referring to the twisting.
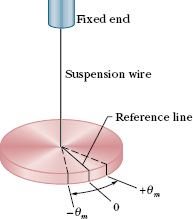
Fig. 15-7 A torsion pendulum is an angular version of a linear simple harmonic oscillator. The disk oscillates in a horizontal plane; the reference line oscillates with angular amplitude θm. The twist in the suspension wire stores potential energy as a spring does and provides the restoring torque.
If we rotate the disk in Fig. 15-7 by some angular displacement θ from its rest position (where the reference line is at θ = 0) and release it, it will oscillate about that position in angular simple harmonic motion. Rotating the disk through an angle θ in either direction introduces a restoring torque given by

Here κ (Greek kappa) is a constant, called the torsion constant, that depends on the length, diameter, and material of the suspension wire.
Comparison of Eq. 15-22 with Eq. 15-10 leads us to suspect that Eq. 15-22 is the angular form of Hooke’s law, and that we can transform Eq. 15-13, which gives the period of linear SHM, into an equation for the period of angular SHM: We replace the spring constant k in Eq. 15-13 with its equivalent, the constant κ of Eq. 15-22, and we replace the mass m in Eq. 15-13 with its equivalent, the rotational inertia I of the oscillating disk. These replacements lead to

which is the correct equation for the period of an angular simple harmonic oscillator, or torsion pendulum.
PROBLEM – SOLVING TACTICS
TACTIC 3: Identifying Angular SHM
When a system undergoes angular simple harmonic motion, its angular acceleration α and angular displacement θ are related by an equation of the form
α = −(a positive constant)θ.
This equation is the angular equivalent of Eq. 15-8 (a = −ω2x). It says that the angular acceleration α is proportional to the angular displacement θ from the equilibrium position but is in the direction opposite the displacement. If you have an expression of this form, you can identify the positive constant as being ω2, and then you can determine ω, f, and T.
You can also identify angular SHM if you have an expression for the torque τ in terms of the angular displacement, because that expression must be in the form of Eq. 15-22 (τ = −κθ) or
τ = −(a positive constant)θ.
This equation is the angular equivalent of Eq. 15-10 (F = −kx). It says that the torque τ is proportional to the angular displacement θ from the equilibrium position but tends to rotate the system in the opposite direction. If you have an expression of this form, then you can identify the positive constant as being the system’s torsion constant κ. If you know the rotational inertia I of the system, you can then determine T.
Figure 15-8a shows a thin rod whose length L is 12.4 cm and whose mass m is 135 g, suspended at its midpoint from a long wire. Its period Ta of angular SHM is measured to be 2.53 s. An irregularly shaped object, which we call object X, is then hung from the same wire, as in Fig. 15-8b, and its period Tb is found to be 4.76 s. What is the rotational inertia of object X about its suspension axis?
Solution: The Key Idea here is that the rotational inertia of either the rod or object X is related to the measured period by Eq. 15-23. In Table 10-2e, the rotational inertia of a thin rod about a perpendicular axis through its midpoint is given as ![]() . Thus, we have, for the rod in Fig. 15-8a,
. Thus, we have, for the rod in Fig. 15-8a,
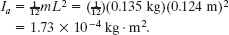
Now let us write Eq. 15-23 twice, once for the rod and once for object X:
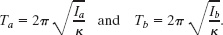
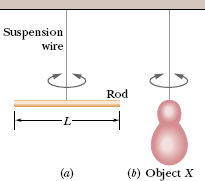
Fig. 15-8 Two torsion pendulums, consisting of (a) a wire and a rod and (b) the same wire and an irregularly shaped object.
The constant κ, which is a property of the wire, is the same for both figures; only the periods and the rotational inertias differ.
Let us square each of these equations, divide the second by the first, and solve the resulting equation for Ib. The result is

Leave a Reply