Figure 14-2a shows a tank of water—or other liquid—open to the atmosphere. As every diver knows, the pressure increases with depth below the air–water interface. The diver’s depth gauge, in fact, is a pressure sensor much like that of Fig. 14-1b. As every mountaineer knows, the pressure decreases with altitude as one ascends into the atmosphere. The pressures encountered by the diver and the mountaineer are usually called hydrostatic pressures, because they are due to fluids that are static (at rest). Here we want to find an expression for hydrostatic pressure as a function of depth or altitude.
Let us look first at the increase in pressure with depth below the water’s surface. We set up a vertical y axis in the tank, with its origin at the air–water interface and the positive direction upward. We next consider a water sample contained in an imaginary right circular cylinder of horizontal base (or face) area A, such that y1 and y2 (both of which are negative numbers) are the depths below the surface of the upper and lower cylinder faces, respectively.
Figure 14-2b shows a free-body diagram for the water in the cylinder. The water is in static equilibrium; that is, it is stationary and the forces on it balance. Three forces act on it vertically: Force 
acts at the top surface of the cylinder and is due to the water above the cylinder. Similarly, force 
acts at the bottom surface of the cylinder and is due to the water below the cylinder. The gravitational force on the water in the cylinder is represented by m
, where m is the mass of the water in the cylinder. The balance of these forces is written as
We want to transform Eq. 14-5 into an equation involving pressures. From Eq. 14-4, we know that
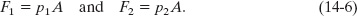
The mass m of the water in the cylinder is, from Eq. 14-2, m = ρV, where the cylinder’s volume V is the product of its face area A and its height y1 − y2. Thus, m is equal to ρA(y1 − y2). Substituting this and Eq. 14-6 into Eq. 14-5, we find
p2A = p1 A + ρAg(y1 − y2)
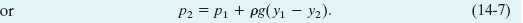
This equation can be used to find pressure both in a liquid (as a function of depth) and in the atmosphere (as a function of altitude or height). For the former, suppose we seek the pressure p at a depth h below the liquid surface. Then we choose level 1 to be the surface, level 2 to be a distance h below it (as in Fig. 14-3), and p0 to represent the atmospheric pressure on the surface. We then substitute
y1 = 0, p1 = p0 and y2 = −h p2 = p
into Eq. 14-7, which becomes
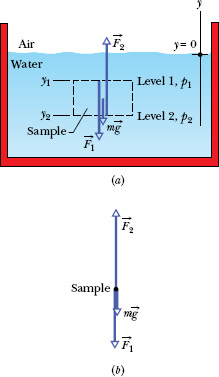
Fig. 14-2 (a) A tank of water in which a sample of water is contained in an imaginary cylinder of horizontal base area A. Force acts at the top surface of the cylinder; force acts at the bottom surface of the cylinder; the gravitational force on the water in the cylinder is represented by m. (b) A free-body diagram of the water sample.
Note that the pressure at a given depth in the liquid depends on that depth but not on any horizontal dimension.
The pressure at a point in a fluid in static equilibrium depends on the depth of that point but not on any horizontal dimension of the fluid or its container.
Thus, Eq. 14-8 holds no matter what the shape of the container. If the bottom surface of the container is at depth h, then Eq. 14-8 gives the pressure p there.
In Eq. 14-8, p is said to be the total pressure, or absolute pressure, at level 2. To see why, note in Fig. 14-3 that the pressure p at level 2 consists of two contributions: (1) p0, the pressure due to the atmosphere, which bears down on the liquid, and (2) ρgh, the pressure due to the liquid above level 2, which bears down on level 2. In general, the difference between an absolute pressure and an atmospheric pressure is called the gauge pressure. (The name comes from the use of a gauge to measure this difference in pressures.) For the situation of Fig. 14-3, the gauge pressure is ρgh.
Equation 14-7 also holds above the liquid surface: It gives the atmospheric pressure at a given distance above level 1 in terms of the atmospheric pressure p1 at level 1 (assuming that the atmospheric density is uniform over that distance). For example, to find the atmospheric pressure at a distance d above level 1 in Fig. 14-3, we substitute
y1 = 0, p1 = p0 and y2 = d, p2 = p.
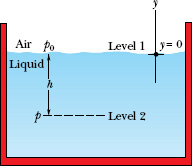
Fig. 14-3 The pressure p increases with depth h below the liquid surface according to Eq. 14-8.
p = p0 − ρair gd.
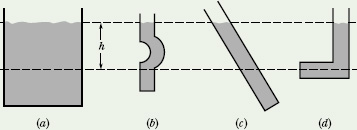
CHECKPOINT 1 The figure shows four containers of olive oil. Rank them according to the pressure at depth h, greatest first.
A novice scuba diver practicing in a swimming pool takes enough air from his tank to fully expand his lungs before abandoning the tank at depth L and swimming to the surface. He ignores instructions and fails to exhale during his ascent. When he reaches the surface, the difference between the external pressure on him and the air pressure in his lungs is 9.3 kPa. From what depth does he start? What potentially lethal danger does he face?
Solution: The Key Idea here is that when the diver fills his lungs at depth L, the external pressure on him (and thus the air pressure within his lungs) is greater than normal and given by Eq. 14-8 as
p = p0 + ρgL,
where p0 is atmospheric pressure and ρ is the water’s density (998 kg/m3, from Table 14-1). As he ascends, the external pressure on him decreases, until it is atmospheric pressure p0 at the surface. His blood pressure also decreases, until it is normal. However, because he does not exhale, the air pressure in his lungs remains at the value it had at depth L. At the surface, the pressure difference between the higher pressure in his lungs and the lower pressure on his chest is
Δp = p − p0 = ρgL,
from which we find
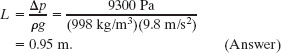
This is not deep! Yet, the pressure difference of 9.3 kPa (about 9% of atmospheric pressure) is sufficient to rupture the diver’s lungs and force air from them into the depressurized blood, which then carries the air to the heart, killing the diver. If the diver follows instructions and gradually exhales as he ascends, he allows the pressure in his lungs to equalize with the external pressure, and then there is no danger.
The ∪-tube in Fig. 14-4 contains two liquids in static equilibrium: Water of density ρw (= 998 kg/m3) is in the right arm, and oil of unknown density ρx is in the left. Measurement gives l = 135 mm and d = 12.3 mm. What is the density of the oil?
Solution: One Key Idea here is that the pressure pint at the level of the oil–water interface in the left arm depends on the density ρx and height of the oil above the interface. A second Key Idea is that the water in the right arm at the same level must be at the same pressure pint. The reason is that, because the water is in static equilibrium, pressures at points in the water at the same level must be the same even if the points are separated horizontally.
In the right arm, the interface is a distance l below the free surface of the water, and we have, from Eq. 14-8,
pint = p0 + ρwgl (right arm).
In the left arm, the interface is a distance l + d below the free surface of the oil, and we have, again from Eq. 14-8,
pint = p0 + ρxg(l + d) (left arm).
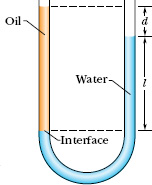
Fig. 14-4 The oil in the left arm stands higher than the water in the right arm because the oil is less dense than the water. Both fluid columns produce the same pressure pint at the level of the interface.
Equating these two expressions and solving for the unknown density yield
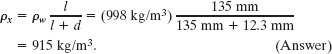
Note that the answer does not depend on the atmospheric pressure p0 or the free-fall acceleration g.
Leave a Reply