When we discuss rigid bodies, we are concerned with particular lumps of matter, such as wooden blocks, baseballs, or metal rods. Physical quantities that we find useful, and in whose terms we express Newton’s laws, are mass and force. We might speak, for example, of a 3.6 kg block acted on by a 25 N force.
With fluids, we are more interested in the extended substance and in properties that can vary from point to point in that substance. It is more useful to speak of density and pressure than of mass and force.
Density
To find the density ρ of a fluid at any point, we isolate a small volume element ΔV around that point and measure the mass Δm of the fluid contained within that element. The density is then
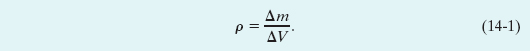
In theory, the density at any point in a fluid is the limit of this ratio as the volume element ΔV at that point is made smaller and smaller. In practice, we assume that a fluid sample is large relative to atomic dimensions and thus is “smooth” (with uniform density), rather than “lumpy” with atoms. This assumption allows us to write Eq. 14-1 as
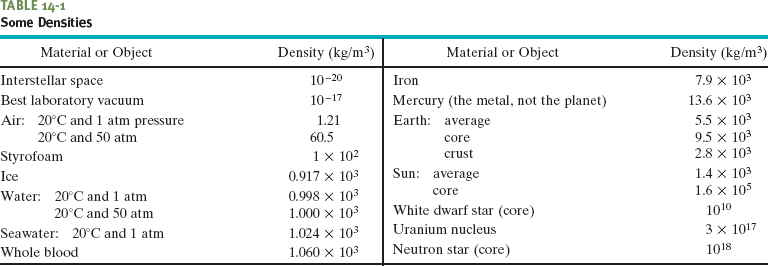
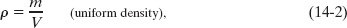
where m and V are the mass and volume of the sample.
Density is a scalar property; its SI unit is the kilogram per cubic meter. Table 14-1 shows the densities of some substances and the average densities of some objects. Note that the density of a gas (see Air in the table) varies considerably with pressure, but the density of a liquid (see Water) does not; that is, gases are readily compressible but liquids are not.
Pressure
Let a small pressure-sensing device be suspended inside a fluid-filled vessel, as in Fig. 14-1a. The sensor (Fig. 14-1b) consists of a piston of surface area ΔA riding in a close-fitting cylinder and resting against a spring. A readout arrangement allows us to record the amount by which the (calibrated) spring is compressed by the surrounding fluid, thus indicating the magnitude ΔF of the force that acts normal to the piston. We define the pressure on the piston from the fluid as
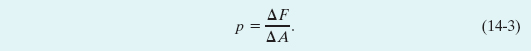
In theory, the pressure at any point in the fluid is the limit of this ratio as the surface area ΔA of the piston, centered on that point, is made smaller and smaller. However, if the force is uniform over a flat area A, we can write Eq. 14-3 as
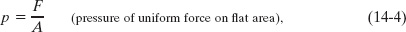
where F is the magnitude of the normal force on area A. (When we say a force is uniform over an area, we mean that the force is evenly distributed over every point of the area.)
We find by experiment that at a given point in a fluid at rest, the pressure p defined by Eq. 14-4 has the same value no matter how the pressure sensor is oriented. Pressure is a scalar, having no directional properties. It is true that the force acting on the piston of our pressure sensor is a vector quantity, but Eq. 14-4 involves only the magnitude of that force, a scalar quantity.
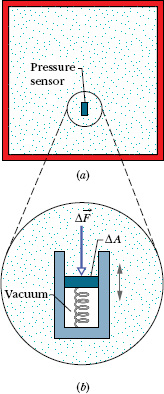
Fig. 14-1 (a) A fluid-filled vessel containing a small pressure sensor, shown in (b). The pressure is measured by the relative position of the movable piston in the sensor.
The SI unit of pressure is the newton per square meter, which is given a special name, the pascal (Pa). In metric countries, tire pressure gauges are calibrated in kilopascals. The pascal is related to some other common (non-SI) pressure units as follows:

1 atm = 1.01 × 105 Pa = 760 torr = 14.7 lb/in.2.
The atmosphere (atm) is, as the name suggests, the approximate average pressure of the atmosphere at sea level. The torr (named for Evangelista Torricelli, who invented the mercury barometer in 1674) was formerly called the millimeter of mercury (mm Hg). The pound per square inch is often abbreviated psi. Table 14-2 shows some pressures.
A living room has floor dimensions of 3.5 m and 4.2 m and a height of 2.4 m.
(a) What does the air in the room weigh when the air pressure is 1.0 atm?
Solution: The Key Ideas here are these: (1) The air’s weight is equal to mg, where m is its mass. (2) Mass m is related to the air density ρ and the air volume V by Eq. 14-2 (ρ = m/V). Putting these two ideas together and taking the density of air at 1.0 atm from Table 14-1, we find
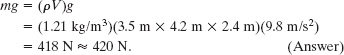
This is the weight of about 110 cans of Pepsi.
(b) What is the magnitude of the atmosphere’s force on the floor of the room?
Solution: The Key Idea here is that the atmosphere pushes down on the floor with a force of magnitude F that is uniform over the floor. Thus, the atmosphere produces a pressure that is related to F and the flat area A of the floor by Eq. 14-4 (p = F/A), which gives us
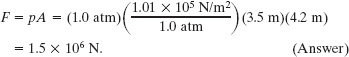
This enormous force is equal to the weight of the column of air that covers the floor and extends all the way to the top of the atmosphere.
Leave a Reply