As a satellite orbits Earth in an elliptical path, both its speed, which fixes its kinetic energy K, and its distance from the center of Earth, which fixes its gravitational potential energy U, fluctuate with fixed periods. However, the mechanical energy E of the satellite remains constant. (Since the satellite’s mass is so much smaller than Earth’s mass, we assign U and E for the Earth–satellite system to the satellite alone.)
The potential energy of the system is given by Eq. 13-21:
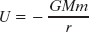
(with U = 0 for infinite separation). Here r is the radius of the satellite’s orbit, assumed for the time being to be circular, and M and m are the masses of Earth and the satellite, respectively.
To find the kinetic energy of a satellite in a circular orbit, we write Newton’s second law (F = ma) as
where v2/r is the centripetal acceleration of the satellite. Then, from Eq. 13-37, the kinetic energy is
which shows us that for a satellite in a circular orbit,
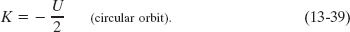
The total mechanical energy of the orbiting satellite is
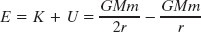
or
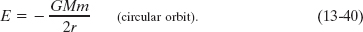
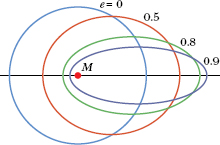
Fig. 13-17 Four orbits with different eccentricities e about an object of mass M. All four orbits have the same semimajor axis a and thus correspond to the same total mechanical energy E.
This tells us that for a satellite in a circular orbit, the total energy E is the negative of the kinetic energy K:
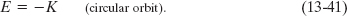
For a satellite in an elliptical orbit of semimajor axis a, we can substitute a for r in Eq. 13-40 to find the mechanical energy:
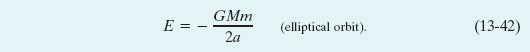
Equation 13-42 tells us that the total energy of an orbiting satellite depends only on the semimajor axis of its orbit and not on its eccentricity e. For example, four orbits with the same semimajor axis are shown in Fig. 13-17; the same satellite would have the same total mechanical energy E in all four orbits. Figure 13-18 shows the variation of K, U, and E with r for a satellite moving in a circular orbit about a massive central body.
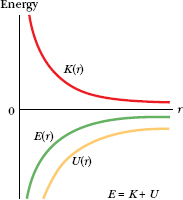
Fig. 13-18 The variation of kinetic energy K, potential energy U, and total energy E with radius r for a satellite in a circular orbit. For any value of r, the values of U and E are negative, the value of K is positive, and E = −K. As r → ∞, all three energy curves approach a value of zero.
CHECKPOINT 6 In the figure here, a space shuttle is initially in a circular orbit of radius r about Earth. At point P, the pilot briefly fires a forward-pointing thruster to decrease the shuttle’s kinetic energy K and mechanical energy E. (a) Which of the dashed elliptical orbits shown in the figure will the shuttle then take? (b) Is the orbital period T of the shuttle (the time to return to P) then greater than, less than, or the same as in the circular orbit?
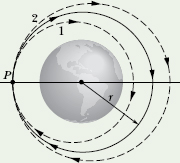
A playful astronaut releases a bowling ball, of mass m = 7.20 kg, into circular orbit about Earth at an altitude h of 350 km.
(a) What is the mechanical energy E of the ball in its orbit?
Solution: The Key Idea here is that we can get E from the orbital energy, given by Eq. 13-40 (E = −GMm/2r), if we first find the orbital radius r. That radius must be
r = R + h = 6370 km + 350 km = 6.72 × 106 m,
in which R is the radius of Earth. Then, from Eq. 13-40, the mechanical energy is
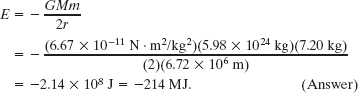
(b) What is the mechanical energy E0 of the ball on the launchpad at Cape Canaveral? From there to the orbit, what is the change ΔE in the ball’s mechanical energy?
Solution: The Key Idea here is that, on the launchpad, the ball is not in orbit and thus Eq. 13-40 does not apply. Instead, we must find E0 = K0 + U0, where K0 is the ball’s kinetic energy and U0 is the gravitational potential energy of the ball–Earth system. To find U0, we use Eq. 13-21 to write
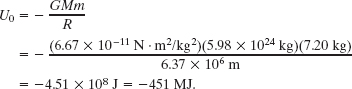
The kinetic energy K0 of the ball is due to the ball’s motion with Earth’s rotation. You can show that K0 is less than 1 MJ, which is negligible relative to U0. Thus, the mechanical energy of the ball on the launchpad is
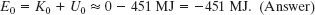
The increase in the mechanical energy of the ball from launchpad to orbit is
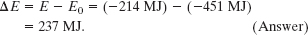
This is worth a few dollars at your utility company. Obviously the high cost of placing objects into orbit is not due to their required mechanical energy.
Leave a Reply