The motions of the planets, as they seemingly wander against the background of the stars, have been a puzzle since the dawn of history. The “loop-the-loop” motion of Mars, shown in Fig. 13-12, was particularly baffling. Johannes Kepler (1571–1630), after a lifetime of study, worked out the empirical laws that govern these motions. Tycho Brahe (1546–1601), the last of the great astronomers to make observations without the help of a telescope, compiled the extensive data from which Kepler was able to derive the three laws of planetary motion that now bear Kepler’s name. Later, Newton (1642–1727) showed that his law of gravitation leads to Kepler’s laws.
In this section we discuss each of Kepler’s three laws. Although here we apply the laws to planets orbiting the Sun, they hold equally well for satellites, either natural or artificial, orbiting Earth or any other massive central body.
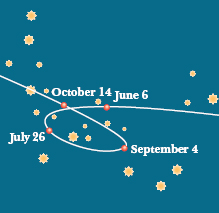
Fig. 13-12 The path seen from Earth for the planet Mars as it moved against a background of the constellation Capricorn during 1971. The planet’s position on four days is marked. Both Mars and Earth are moving in orbits around the Sun so that we see the position of Mars relative to us; this relative motion sometimes results in an apparent loop in the path of Mars.
1. THE LAW OF ORBITS: All planets move in elliptical orbits, with the Sun at one focus.
Figure 13-13 shows a planet of mass m moving in such an orbit around the Sun, whose mass is M. We assume that M 
m, so that the center of mass of the planet–Sun system is approximately at the center of the Sun.
The orbit in Fig. 13-13 is described by giving its semimajor axis a and its eccentricity e, the latter defined so that ea is the distance from the center of the ellipse to either focus F or F′. An eccentricity of zero corresponds to a circle, in which the two foci merge to a single central point. The eccentricities of the planetary orbits are not large; so if the orbits are drawn to scale, they look circular. The eccentricity of the ellipse of Fig. 13-13, which has been exaggerated for clarity, is 0.74. The eccentricity of Earth’s orbit is only 0.0167.
2. THE LAW OF AREAS: A line that connects a planet to the Sun sweeps out equal areas in the plane of the planet’s orbit in equal time intervals; that is, the rate dA/dt at which it sweeps out area A is constant.
Qualitatively, this second law tells us that the planet will move most slowly when it is farthest from the Sun and most rapidly when it is nearest to the Sun. As it turns out, Kepler’s second law is totally equivalent to the law of conservation of angular momentum. Let us prove it.
The area of the shaded wedge in Fig. 13-14a closely approximates the area swept out in time Δt by a line connecting the Sun and the planet, which are separated by distance r. The area ΔA of the wedge is approximately the area of a triangle with base r Δθ and height r. Since the area of a triangle is one-half of the base times the height, ΔA ≈ 
r2 Δθ. This expression for ΔA becomes more exact as Δt (hence Δθ) approaches zero. The instantaneous rate at which area is being swept out is then
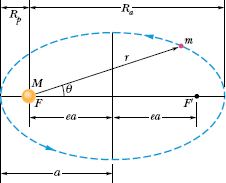
Fig. 13-13 A planet of mass m moving in an elliptical orbit around the Sun. The Sun, of mass M, is at one focus F of the ellipse. The other focus is F′, which is located in empty space. Each focus is a distance ea from the ellipse’s center, with e being the eccentricity of the ellipse. The semimajor axis a of the ellipse, the perihelion (nearest the Sun) distance Rp, and the aphelion (farthest from the Sun) distance Ra are also shown.
in which ω is the angular speed of the rotating line connecting Sun and planet.
Figure 13-14b shows the linear momentum 
of the planet, along with the radial and perpendicular components of . From Eq. 11-20 (L = rp┴), the magnitude of the angular momentum 
of the planet about the Sun is given by the product of r and p┴, the component of perpendicular to r. Here, for a planet of mass m,
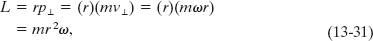
where we have replaced v┴ with its equivalent ωr(Eq. 10-18). Eliminating r2ω between Eqs. 13-30 and 13-31 leads to
If dA/dt is constant, as Kepler said it is, then Eq. 13-32 means that L must also be constant—angular momentum is conserved. Kepler’s second law is indeed equivalent to the law of conservation of angular momentum.
3. THE LAW OF PERIODS: The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit.
To see this, consider the circular orbit of Fig. 13-15, with radius r (the radius of a circle is equivalent to the semimajor axis of an ellipse). Applying Newton’s second law (F = ma) to the orbiting planet in Fig. 13-15 yields
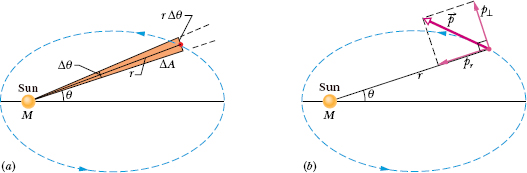
Fig. 13-14 (a) In time Δt, the line r connecting the planet to the Sun moves through an angle Δθ, sweeping out an area ΔA (shaded). (b) The linear momentum of the planet and the components of .
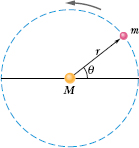
Fig. 13-15 A planet of mass m moving around the Sun in a circular orbit of radius r.
Here we have substituted from Eq. 13-1 for the force magnitude F and used Eq. 10-23 to substitute ω2r for the centripetal acceleration. If we now use Eq. 10-20 to replace ω with 2π/T, where T is the period of the motion, we obtain Kepler’s third law:
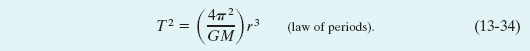
The quantity in parentheses is a constant that depends only on the mass M of the central body about which the planet orbits.
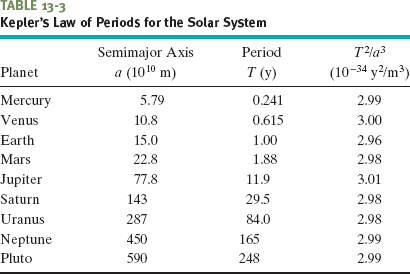
Equation 13-34 holds also for elliptical orbits, provided we replace r with a, the semimajor axis of the ellipse. This law predicts that the ratio T2/a3 has essentially the same value for every planetary orbit around a given massive body. Table 13-3 shows how well it holds for the orbits of the planets of the solar system.
CHECKPOINT 5 Satellite 1 is in a certain circular orbit around a planet, while satellite 2 is in a larger circular orbit. Which satellite has (a) the longer period and (b) the greater speed?
Comet Halley orbits the Sun with a period of 76 years and, in 1986, had a distance of closest approach to the Sun, its perihelion distance Rp, of 8.9 × 1010 m. Table 13-3 shows that this is between the orbits of Mercury and Venus.
(a) What is the comet’s farthest distance from the Sun, which is called its aphelion distance Ra?
Solution: One Key Idea comes from Fig. 13-13, in which we see that Ra + Rp = 2a, where a is the semimajor axis of the orbit. Thus, we can find Ra if we first find a. A second Key Idea is that we can relate a to the given period via the law of periods (Eq. 13-34) if we simply substitute the semimajor axis a for r. Doing so and then solving for a, we have
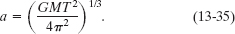
If we substitute the mass M of the Sun, 1.99 × 1030 kg, and the period T of the comet, 76 years or 2.4 × 109 s, into Eq. 13-35, we find that a = 2.7 × 1012 m. Now we have
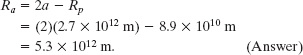
Table 13-3 shows that this is a little less than the semimajor axis of the orbit of Pluto. Thus, the comet does not get farther from the Sun than Pluto.
(b) What is the eccentricity e of the orbit of comet Halley?
Solution: The Key Idea here is that we can relate e, a, and Rp via Fig. 13-13. We see there that ea = a − Rp, or
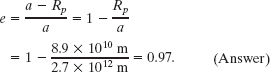
This tells us that, with an eccentricity approaching unity, this orbit must be a long thin ellipse.
Let’s return to the story that opens this lesson. Figure 13-16 shows the observed orbit of the star S2 as the star moves around a mysterious and unobserved object called Sagittarius A* (pronounced “A star”), which is at the center of the Milky Way galaxy. S2 orbits Sagittarius A* with a period of T = 15.2 y and with a semimajor axis of a = 5.50 light-days (= 1.42 × 1014 m). What is the mass M of Sagittarius A*? What is Sagittarius A*?
Solution: The Key Idea here is that the period T and the semimajor axis a of the orbit are related to the mass M of Sagittarius A* according to Kepler’s law of periods. From Eq. 13-34, with a replacing the radius r of a circular orbit, we have
Solving for M and substituting the given data lead us to
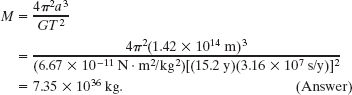
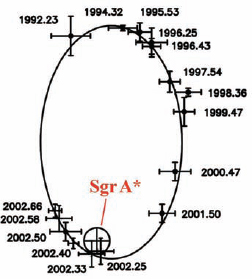
Fig. 13-16 The orbit of star S2 about Sagittarius A* (Sgr A*). The elliptical orbit appears skewed because we do not see it from directly above the orbital plane. The observation dates are given in decimal fractions of a year. Uncertainties in the location of S2 are indicated by the cross bars. Uncertainty in the location of Sgr A* is indicated by the encircled cross bars.
To figure out what Sagittarius A* might be, let’s divide this mass by the mass of our Sun (Msun = 1.99 × 1030 kg) to find that
M = (3.7 × 106)Msun.
Sagittarius A* has a mass of 3.7 million Suns! However, it cannot be seen. Thus, it is an extremely compact object. Such a huge mass in such a small object leads to the reasonable conclusion that this object is a supermassive black hole. In fact, evidence is mounting that a supermassive black hole lurks at the center of most galaxies. (Movies of the stars orbiting Sagittarius A* are available on the Web; search under “black hole galactic center.”)
Leave a Reply