In Section 8-4, we discussed the gravitational potential energy of a particle–Earth system. We were careful to keep the particle near Earth’s surface, so that we could regard the gravitational force as constant. We then chose some reference configuration of the system as having a gravitational potential energy of zero. Often, in this configuration the particle was on Earth’s surface. For particles not on Earth’s surface, the gravitational potential energy decreased when the separation between the particle and Earth decreased.
Here, we broaden our view and consider the gravitational potential energy U of two particles, of masses m and M, separated by a distance r. We again choose a reference configuration with U equal to zero. However, to simplify the equations, the separation distance r in the reference configuration is now large enough to be approximated as infinite. As before, the gravitational potential energy decreases when the separation decreases. Since U = 0 for r = ∞, the potential energy is negative for any finite separation and becomes progressively more negative as the particles move closer together.
With these facts in mind and as we shall justify next, we take the gravitational potential energy of the two-particle system to be
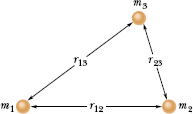
Fig. 13-9 A system consisting of three particles. The gravitational potential energy of the system is the sum of the gravitational potential energies of all three pairs of particles.
Note that U(r) approaches zero as r approaches infinity and that for any finite value of r, the value of U(r) is negative.
The potential energy given by Eq. 13-21 is a property of the system of two particles rather than of either particle alone. There is no way to divide this energy and say that so much belongs to one particle and so much to the other. However, if M 
m, as is true for Earth (mass M) and a baseball (mass m), we often speak of “the potential energy of the baseball.” We can get away with this because, when a baseball moves in the vicinity of Earth, changes in the potential energy of the baseball–Earth system appear almost entirely as changes in the kinetic energy of the baseball, since changes in the kinetic energy of Earth are too small to be measured. Similarly, in Section 13-8 we shall speak of “the potential energy of an artificial satellite” orbiting Earth, because the satellite’s mass is so much smaller than Earth’s mass. When we speak of the potential energy of bodies of comparable mass, however, we have to be careful to treat them as a system.
If our system contains more than two particles, we consider each pair of particles in turn, calculate the gravitational potential energy of that pair with Eq. 13-21 as if the other particles were not there, and then algebraically sum the results. Applying Eq. 13-21 to each of the three pairs of Fig. 13-9, for example, gives the potential energy of the system as
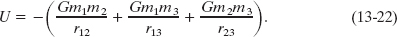
Proof of Equation 13-21
Let us shoot a baseball directly away from Earth along the path in Fig. 13-10. We want to find an expression for the gravitational potential energy U of the ball at point P along its path, at radial distance R from Earth’s center. To do so, we first find the work W done on the ball by the gravitational force as the ball travels from point P to a great (infinite) distance from Earth. Because the gravitational force 
(r) is a variable force (its magnitude depends on r), we must use the techniques of Section 7-8 to find the work. In vector notation, we can write
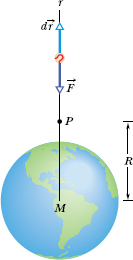
Fig. 13-10 A baseball is shot directly away from Earth, through point P at radial distance R from Earth’s center. The gravitational force on the ball and a differential displacement vector d
are shown, both directed along a radial r axis.
The integral contains the scalar (or dot) product of the force (r) and the differential displacement vector d along the ball’s path. We can expand that product as
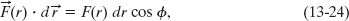
where ϕ is the angle between the directions of (r) and d. When we substitute 180° for ϕ and Eq. 13-1 for F(r), Eq. 13-24 becomes
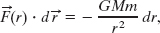
where M is Earth’s mass and m is the mass of the ball.
Substituting this into Eq. 13-23 and integrating gives us
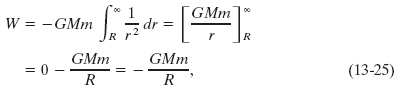
Fig. 13-11 Near Earth, a baseball is moved from point A to point G along a path consisting of radial lengths and circular arcs.
where W is the work required to move the ball from point P (at distance R) to infinity. Equation 8-1 (ΔU = −W) tells us that we can also write that work in terms of potential energies as
U∞ − U = −W.
Because the potential energy U∞ at infinity is zero, U is the potential energy at P, and W is given by Eq. 13-25, this equation becomes
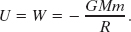
Switching R to r gives us Eq. 13-21, which we set out to prove.
Path Independence
In Fig. 13-11, we move a baseball from point A to point G along a path consisting of three radial lengths and three circular arcs (centered on Earth). We are interested in the total work W done by Earth’s gravitational force on the ball as it moves from A to G. The work done along each circular arc is zero, because the direction of is perpendicular to the arc at every point. Thus, W is the sum of only the works done by along the three radial lengths.
Now, suppose we mentally shrink the arcs to zero. We would then be moving the ball directly from A to G along a single radial length. Does that change W? No. Because no work was done along the arcs, eliminating them does not change the work. The path taken from A to G now is clearly different, but the work done by is the same.
We discussed such a result in a general way in Section 8-3. Here is the point: The gravitational force is a conservative force. Thus, the work done by the gravitational force on a particle moving from an initial point i to a final point f is independent of the path taken between the points. From Eq. 8-1, the change ΔU in the gravitational potential energy from point i to point f is given by
Since the work W done by a conservative force is independent of the actual path taken, the change ΔU in gravitational potential energy is also independent of the path taken.
Potential Energy and Force
In the proof of Eq. 13-21, we derived the potential energy function U(r) from the force function (r). We should be able to go the other way—that is, to start from the potential energy function and derive the force function. Guided by Eq. 8-22 (F(x) = −dU(x)/dx), we can write
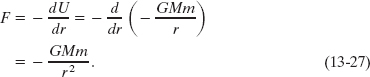
This is Newton’s law of gravitation (Eq. 13-1). The minus sign indicates that the force on mass m points radially inward, toward mass M.
Escape Speed
If you fire a projectile upward, usually it will slow, stop momentarily, and return to Earth. There is, however, a certain minimum initial speed that will cause it to move upward forever, theoretically coming to rest only at infinity. This minimum initial speed is called the (Earth) escape speed.
Consider a projectile of mass m, leaving the surface of a planet (or some other astronomical body or system) with escape speed v. The projectile has a kinetic energy K given by 
mv2 and a potential energy U given by Eq. 13-21:
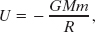
in which M is the mass of the planet and R is its radius.
When the projectile reaches infinity, it stops and thus has no kinetic energy. It also has no potential energy because an infinite separation between two bodies is our zero-potential-energy configuration. Its total energy at infinity is therefore zero. From the principle of conservation of energy, its total energy at the planet’s surface must also have been zero, and so
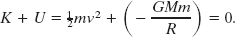
This yields
Note that v does not depend on the direction in which a projectile is fired from a planet. However, attaining that speed is easier if the projectile is fired in the direction the launch site is moving as the planet rotates about its axis. For example, rockets are launched eastward at Cape Canaveral to take advantage of the Cape’s eastward speed of 1500 km/h due to Earth’s rotation.
Equation 13-28 can be applied to find the escape speed of a projectile from any astronomical body, provided we substitute the mass of the body for M and the radius of the body for R. Table 13-2 shows some escape speeds.
CHECKPOINT 4 You move a ball of mass m away from a sphere of mass M. (a) Does the gravitational potential energy of the ball–sphere system increase or decrease? (b) Is positive or negative work done by the gravitational force between the ball and the sphere?
An asteroid, headed directly toward Earth, has a speed of 12 km/s relative to the planet when the asteroid is 10 Earth radii from Earth’s center. Neglecting the effects of Earth’s atmosphere on the asteroid, find the asteroid’s speed vf when it reaches Earth’s surface.
Solution: One Key Idea is that, because we are to neglect the effects of the atmosphere on the asteroid, the mechanical energy of the asteroid–Earth system is conserved during the fall. Thus, the final mechanical energy (when the asteroid reaches Earth’s surface) is equal to the initial mechanical energy. With kinetic energy K and gravitational potential energy U, we can write this as
A second Key Idea is that, if we assume the system is isolated, the system’s linear momentum must be conserved during the fall. Therefore, the momentum change of the asteroid and that of Earth must be equal in magnitude and opposite in sign. However, because Earth’s mass is so much greater than the asteroid’s mass, the change in Earth’s speed is negligible relative to the change in the asteroid’s speed. So, the change in Earth’s kinetic energy is also negligible. Thus, we can assume that the kinetic energies in Eq. 13-29 are those of the asteroid alone.
Let m represent the asteroid’s mass and M represent Earth’s mass (5.98 × 1024 kg). The asteroid is initially at distance 10RE and finally at distance RE, where RE is Earth’s radius (6.37 × 106 m). Substituting Eq. 13-21 for U and mv2 for K, we rewrite Eq. 13-29 as
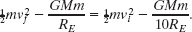
Rearranging and substituting known values, we find
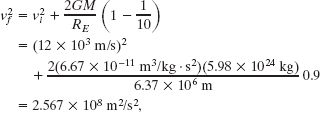
and
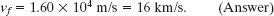
At this speed, the asteroid would not have to be particularly large to do considerable damage at impact. If it were only 5 m across, the impact could release about as much energy as the nuclear explosion at Hiroshima. Alarmingly, about 500 million asteroids of this size are near Earth’s orbit, and in 1994 one of them apparently penetrated Earth’s atmosphere and exploded 20 km above the South Pacific (setting off nuclear-explosion warnings on six military satellites). The impact of an asteroid 500 m across (there may be a million of them near Earth’s orbit) could end modern civilization and almost eliminate humans worldwide.
Leave a Reply