Given a group of particles, we find the net (or resultant) gravitational force on any one of them from the others by using the principle of superposition. This is a general principle that says a net effect is the sum of the individual effects. Here, the principle means that we first compute the individual gravitational forces that act on our selected particle due to each of the other particles. We then find the net force by adding these forces vectorially, as usual.
For n interacting particles, we can write the principle of superposition for the gravitational forces on particle 1 as
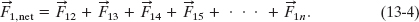
Here 
is the net force on particle 1 and, for example, 
is the force on particle 1 from particle 3. We can express this equation more compactly as a vector sum:
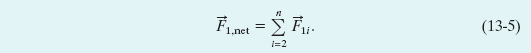
What about the gravitational force on a particle from a real (extended) object? This force is found by dividing the object into parts small enough to treat as particles and then using Eq. 13-5 to find the vector sum of the forces on the particle from all the parts. In the limiting case, we can divide the extended object into differential parts each of mass dm and each producing a differential force d
on the particle. In this limit, the sum of Eq. 13-5 becomes an integral and we have
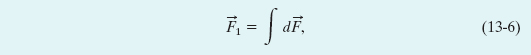
in which the integral is taken over the entire extended object and we drop the subscript “net.” If the extended object is a uniform sphere or a spherical shell, we can avoid the integration of Eq. 13-6 by assuming that the object’s mass is concentrated at the object’s center and using Eq. 13-1.
Figure 13-4a shows an arrangement of three particles, particle 1 of mass m1 = 6.0 kg and particles 2 and 3 of mass m2 = m3 = 4.0 kg, and distance a = 2.0 cm. What is the net gravitational force 
on particle 1 due to the other particles?
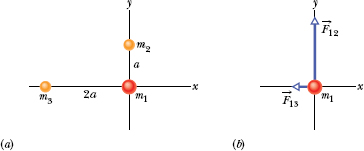
Fig. 13-4 (a) An arrangement of three particles. (b) The forces acting on the particle of mass m1 due to the other particles.
Solution: One Key Idea here is that, because we have particles, the magnitude of the gravitational force on particle 1 due to either of the other particles is given by Eq. 13-1 (F = Gm1 m2/r2). Thus, the magnitude of the force 
on particle 1 from particle 2 is
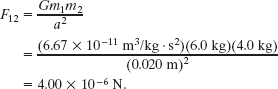
Similarly, the magnitude of force on particle 1 from particle 3 is
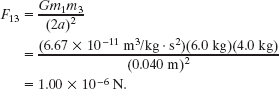
To determine the directions of and , we use this Key Idea: Each force on particle 1 is directed toward the particle responsible for that force. Thus, is directed in the positive direction of the y axis (Fig. 13-4b) and has only the y component F12. Similarly, is directed in the negative direction of the x axis and has only the x component −F13.
To find the net force on particle 1, we first use this very important Key Idea: Because the forces are not directed along the same line, we cannot simply add or subtract their magnitudes or their components to get their net force. Instead, we must add them as vectors.
We can do so on a vector-capable calculator. However, here we note that −F13 and F12 are actually the x and y components of . Therefore, we can use Eq. 3-6 to find first the magnitude and then the direction of . The magnitude is
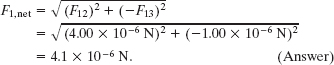
Relative to the positive direction of the x axis, Eq. 3-6 gives the direction of as
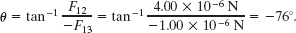
Is this a reasonable direction? No, because the direction of must be between the directions of and . Recall from lesson 3 (Problem-Solving Tactic 3) that a calculator displays only one of the two possible answers to a tan−1 function. We find the other answer by adding 180°:
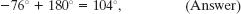
which is a reasonable direction for .
CHECKPOINT 2 The figure shows four arrangements of three particles of equal masses. (a) Rank the arrangements according to the magnitude of the net gravitational force on the particle labeled m, greatest first. (b) In arrangement 2, is the direction of the net force closer to the line of length d or to the line of length D?
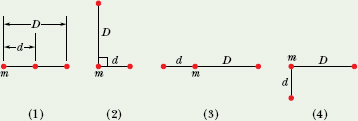
Figure 13-5a shows an arrangement of five particles, with masses m1 = 8.0 kg, m2 = m3 = m4 = m5 = 2.0 kg, and with a = 2.0 cm and θ = 30°. What is the net gravitational force on particle 1 due to the other particles?
Solution: Our Key Ideas are the same as in Sample Problem 13-1. However, this problem has a lot of symmetry that can help simplify the solution.
For the magnitudes of the forces on particle 1, first note that particles 2 and 4 have equal masses and equal distances of r = 2a from particle 1. Thus, from Eq. 13-1, we find
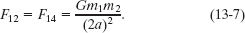
Similarly, since particles 3 and 5 have equal masses and are both distance r = a from particle 1, we find
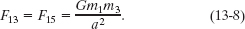
We could now substitute known data into these two equations to evaluate the magnitudes of the forces, indicate the directions of the forces on the free-body diagram of Fig. 13-5b, and then find the net force either (1) by resolving the vectors into x and y components, finding the net x and net y components, and then vectorially combining them or (2) by adding the vectors directly on a vector-capable calculator.
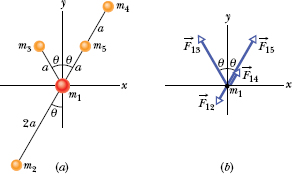
Fig. 13-5 (a) An arrangement of five particles. (b) The forces acting on the particle of mass m1 due to the other four particles.
Instead, however, we shall make further use of the symmetry of the problem. First, we note that and 
are equal in magnitude but opposite in direction; thus, those forces cancel. Inspection of Fig. 13-5b and Eq. 13-8 reveals that the x components of and 
also cancel, and that their y components are identical in magnitude and both act in the positive direction of the y axis. Thus, acts in that same direction, and its magnitude is twice the y component of :
Note that the presence of particle 5 along the line between particles 1 and 4 does not alter the gravitational force on particle 1 from particle 4.
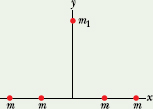
CHECKPOINT 3 In the figure here, what is the direction of the net gravitational force on the particle of mass m1 due to the other particles, each of mass m and arranged symmetrically relative to the y axis?
PROBLEM – SOLVING TACTICS
TACTIC 1: Drawing Gravitational Force Vectors
When you are given a diagram of particles, such as Fig. 13-4a, and asked to find the net gravitational force on one of them, you should usually draw a free-body diagram showing only the particle of concern and the forces on it alone, as in Fig. 13-4b. If, instead, you choose to superimpose the force vectors on the given diagram, be sure to draw the vectors with either all tails (preferably) or all heads on the particle experiencing those forces. If you draw the vectors elsewhere, you invite confusion—and confusion is guaranteed if you draw the vectors on the particles causing the forces.
TACTIC 2: Simplifying a Sum of Forces with Symmetry
In Sample Problem 13-2 we used the symmetry of the situation: By realizing that particles 2 and 4 are positioned symmetrically about particle 1, and thus that and cancel, we avoided calculating either force. By realizing that the x components of and cancel and that their y components are identical and add, we saved even more effort.
In problems with symmetry, you can save much effort and reduce the chance of error by identifying which calculations are not needed because of the symmetry. Such identification is a skill acquired only by doing many homework problems.
Leave a Reply