Principle of Equivalence
Albert Einstein once said: “I was . . . in the patent office at Bern when all of a sudden a thought occurred to me: ‘If a person falls freely, he will not feel his own weight.’ I was startled. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.”
Thus Einstein tells us how he began to form his general theory of relativity. The fundamental postulate of this theory about gravitation (the gravitating of objects toward each other) is called the principle of equivalence, which says that gravitation and acceleration are equivalent. If a physicist were locked up in a small box as in Fig. 13-19, he would not be able to tell whether the box was at rest on Earth (and subject only to Earth’s gravitational force), as in Fig. 13-19a, or accelerating through interstellar space at 9.8 m/s2 (and subject only to the force producing that acceleration), as in Fig. 13-19b. In both situations he would feel the same and would read the same value for his weight on a scale. Moreover, if he watched an object fall past him, the object would have the same acceleration relative to him in both situations.
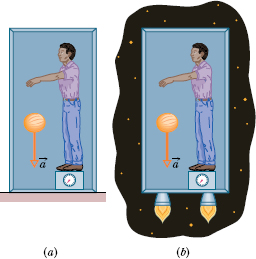
Fig. 13-19 (a) A physicist in a box resting on Earth sees a cantaloupe falling with acceleration a = 9.8 m/s2. (b) If he and the box accelerate in deep space at 9.8 m/s2, the cantaloupe has the same acceleration relative to him. It is not possible, by doing experiments within the box, for the physicist to tell which situation he is in. For example, the platform scale on which he stands reads the same weight in both situations.
Curvature of Space
We have thus far explained gravitation as due to a force between masses. Einstein showed that, instead, gravitation is due to a curvature of space that is caused by the masses. (As is discussed later in this app, space and time are entangled, so the curvature of which Einstein spoke is really a curvature of spacetime, the combined four dimensions of our universe.)
Picturing how space (such as vacuum) can have curvature is difficult. An analogy might help: Suppose that from orbit we watch a race in which two boats begin on Earth’s equator with a separation of 20 km and head due south (Fig. 13-20a). To the sailors, the boats travel along flat, parallel paths. However, with time the boats draw together until, nearer the south pole, they touch. The sailors in the boats can interpret this drawing together in terms of a force acting on the boats. Looking on from space, however, we can see that the boats draw together simply because of the curvature of Earth’s surface. We can see this because we are viewing the race from “outside” that surface.
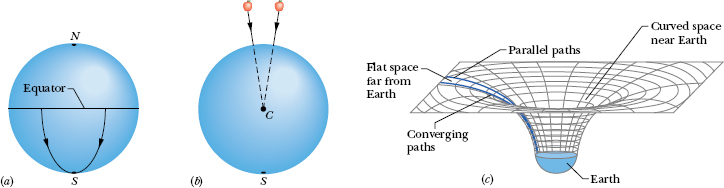
Fig. 13-20 (a) Two objects moving along lines of longitude toward the south pole converge because of the curvature of Earth’s surface. (b) Two objects falling freely near Earth move along lines that converge toward the center of Earth because of the curvature of space near Earth. (c) Far from Earth (and other masses), space is flat and parallel paths remain parallel. Close to Earth, the parallel paths begin to converge because space is curved by Earth’s mass.
Figure 13-20b shows a similar race: Two horizontally separated apples are dropped from the same height above Earth. Although the apples may appear to travel along parallel paths, they actually move toward each other because they both fall toward Earth’s center. We can interpret the motion of the apples in terms of the gravitational force on the apples from Earth. We can also interpret the motion in terms of a curvature of the space near Earth, a curvature due to the presence of Earth’s mass. This time we cannot see the curvature because we cannot get “outside” the curved space, as we got “outside” the curved Earth in the boat example. However, we can depict the curvature with a drawing like Fig. 13-20c; there the apples would move along a surface that curves toward Earth because of Earth’s mass.
When light passes near Earth, the path of the light bends slightly because of the curvature of space there, an effect called gravitational lensing. When light passes a more massive structure, like a galaxy or a black hole having large mass, its path can be bent more. If such a massive structure is between us and a quasar (an extremely bright, extremely distant source of light), the light from the quasar can bend around the massive structure and toward us (Fig. 13-21a). Then, because the light seems to be coming to us from a number of slightly different directions in the sky, we see the same quasar in all those different directions. In some situations, the quasars we see blend together to form a giant luminous arc, which is called an Einstein ring (Fig. 13-21b).
Should we attribute gravitation to the curvature of spacetime due to the presence of masses or to a force between masses? Or should we attribute it to the actions of a type of fundamental particle called a graviton, as conjectured in some modern physics theories? We just don’t know.
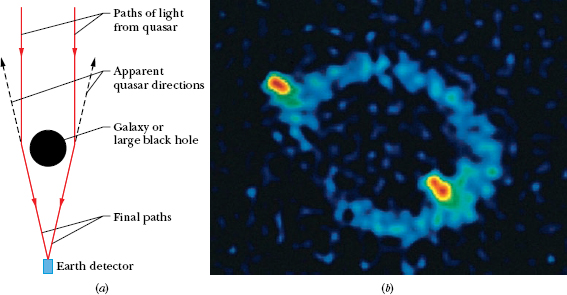
Fig. 13-21 (a) Light from a distant quasar follows curved paths around a galaxy or a large black hole because the mass of the galaxy or black hole has curved the adjacent space. If the light is detected, it appears to have originated along the backward extensions of the final paths (dashed lines). (b) The Einstein ring known as MG1131+0456 on the computer screen of a telescope. The source of the light (actually, radio waves, which are a form of invisible light) is far behind the large, unseen galaxy that produces the ring; a portion of the source appears as the two bright spots seen along the ring.
Leave a Reply