The Requirements of Equilibrium

The translational motion of a body is governed by Newton’s second law in its linear momentum form, given by Eq. 9-27 as

If the body is in translational equilibrium—that is, if  is a constant—then d/dt = 0 and we must have

The rotational motion of a body is governed by Newton’s second law in its angular momentum form, given by Eq. 11-29 as

If the body is in rotational equilibrium—that is, if  is a constant—then d/dt = 0 and we must have

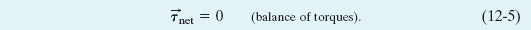
Thus, the two requirements for a body to be in equilibrium are as follows:

 1. The vector sum of all the external forces that act on the body must be zero.

2. The vector sum of all the external torques that act on the body, measured about any possible point, must also be zero.

These requirements obviously hold for static equilibrium. They also hold for the more general equilibrium in which  and  are constant but not zero.

Equations 12-3 and 12-5, as vector equations, are each equivalent to three independent component equations, one for each direction of the coordinate axes:

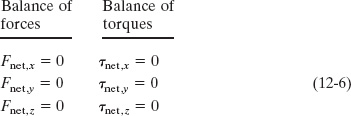
We shall simplify matters by considering only situations in which the forces that act on the body lie in the xy plane. This means that the only torques that can act on the body must tend to cause rotation around an axis parallel to the z axis. With this assumption, we eliminate one force equation and two torque equations from Eqs. 12-6, leaving

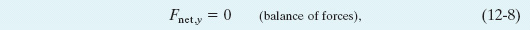
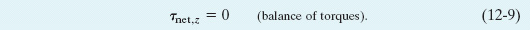
Here, τ_net,z is the net torque that the external forces produce either about the z axis or about any axis parallel to it.

A hockey puck sliding at constant velocity over ice satisfies Eqs. 12-7, 12-8, and 12-9 and is thus in equilibrium but not in static equilibrium. For static equilibrium, the linear momentum  of the puck must be not only constant but also zero; the puck must be at rest on the ice. Thus, there is another requirement for static equilibrium:

 3. The linear momentum  of the body must be zero.

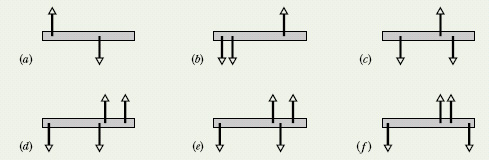
CHECKPOINT 1   The figure gives six overhead views of a uniform rod on which two or more forces act perpendicularly to the rod. If the magnitudes of the forces are adjusted properly (but kept nonzero), in which situations can the rod be in static equilibrium?