The Center of Gravity

The gravitational force on an extended body is the vector sum of the gravitational forces acting on the individual elements (the atoms) of the body. Instead of considering all those individual elements, we can say that

 The gravitational force  on a body effectively acts at a single point, called the center of gravity (cog) of the body.

Here the word “effectively” means that if the forces on the individual elements were somehow turned off and force  at the center of gravity were turned on, the net force and the net torque (about any point) acting on the body would not change.

Until now, we have assumed that the gravitational force  acts at the center of mass (com) of the body. This is equivalent to assuming that the center of gravity is at the center of mass. Recall that, for a body of mass M, the force  is equal to M, where  is the acceleration that the force would produce if the body were to fall freely. In the proof that follows, we show that

 If  is the same for all elements of a body, then the body’s center of gravity (cog) is coincident with the body’s center of mass (com).

This is approximately true for everyday objects because  varies only a little along Earth’s surface and decreases in magnitude only slightly with altitude. Thus, for objects like a mouse or a moose, we have been justified in assuming that the gravitational force acts at the center of mass. After the following proof, we shall resume that assumption.

Proof

First, we consider the individual elements of the body. Figure 12-4a shows an extended body, of mass M, and one of its elements, of mass m_i. A gravitational force  acts on each such element and is equal to m_i. The subscript on  means  is the gravitational acceleration at the location of the element i (it can be different for other elements).

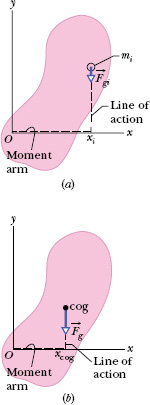
Fig. 12-4   (a) An element of mass m_i in an extended body. The gravitational force  on the element has moment arm x_i about the origin O of the coordinate system. (b) The gravitational force  on a body is said to act at the center of gravity (cog) of the body. Here  has momoment arm x_cog about origin O.

In Fig. 12-4a, each force  produces a torque τ_i on the element about the origin O, with moment arm x_i. Using Eq. 10-41 (τ = r _┴ F), we can write torque τ_i as

The net torque on all the elements of the body is then

Next, we consider the body as a whole. Figure 12-4b shows the gravitational force  acting at the body’s center of gravity. This force produces a torque τ on the body about O, with moment arm x_cog. Again using Eq. 10-41, we can write this torque as

The gravitational force  on the body is equal to the sum of the gravitational forces  on all its elements, so we can substitute ΣF_gi for F_g in Eq. 12-12 to write

Now recall that the torque due to force  acting at the center of gravity is equal to the net torque due to all the forces  acting on all the elements of the body. (That is how we defined the center of gravity.) Thus, τ in Eq. 12-13 is equal to τ_net in Eq. 12-11. Putting those two equations together, we can write

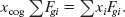
Substituting m_ig_i for F_gi gives us

Now here is a key idea: If the accelerations g_i at all the locations of the elements are the same, we can cancel g_i from this equation to write

The sum Σm_i of the masses of all the elements is the mass M of the body. Therefore, we can rewrite Eq. 12-15 as

The right side of this equation gives the coordinate x_com of the body’s center of mass (Eq. 9-4). We now have what we sought to prove:

CHECKPOINT 2   Suppose that you skewer an apple with a thin rod, missing the apple’s center of gravity. When you hold the rod horizontally and allow the apple to rotate freely, where does the center of gravity end up and why?