Indeterminate Structures

For the problems of this lesson, we have only three independent equations at our disposal, usually two balance of forces equations and one balance of torques equation about a given rotation axis. Thus, if a problem has more than three unknowns, we cannot solve it.

It is easy to find such problems. In Sample Problem 12-2, for example, we could have assumed that there is friction between the wall and the top of the ladder. Then there would have been a vertical frictional force acting where the ladder touches the wall, making a total of four unknown forces. With only three equations, we could not have solved this problem.

Consider also an unsymmetrically loaded car. What are the forces—all different—on the four tires? Again, we cannot find them because we have only three independent equations with which to work. Similarly, we can solve an equilibrium problem for a table with three legs but not for one with four legs. Problems like these, in which there are more unknowns than equations, are called indeterminate.

Yet solutions to indeterminate problems exist in the real world. If you rest the tires of the car on four platform scales, each scale will register a definite reading, the sum of the readings being the weight of the car. What is eluding us in our efforts to find the individual forces by solving equations?

The problem is that we have assumed—without making a great point of it— that the bodies to which we apply the equations of static equilibrium are perfectly rigid. By this we mean that they do not deform when forces are applied to them. Strictly, there are no such bodies. The tires of the car, for example, deform easily under load until the car settles into a position of static equilibrium.

We have all had experience with a wobbly restaurant table, which we usually level by putting folded paper under one of the legs. If a big enough elephant sat on such a table, however, you may be sure that if the table did not collapse, it would deform just like the tires of a car. Its legs would all touch the floor, the forces acting upward on the table legs would all assume definite (and different) values as in Fig. 12-9, and the table would no longer wobble. How do we find the values of those forces acting on the legs?

To solve such indeterminate equilibrium problems, we must supplement equilibrium equations with some knowledge of elasticity, the branch of physics and engineering that describes how real bodies deform when forces are applied to them. The next section provides an introduction to this subject.

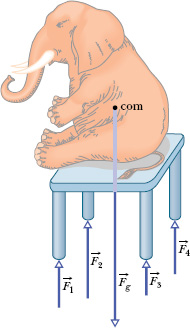
Fig. 12-9   The table is an indeterminate structure. The four forces on the table legs differ from one another in magnitude and cannot be found from the laws of static equilibrium alone.

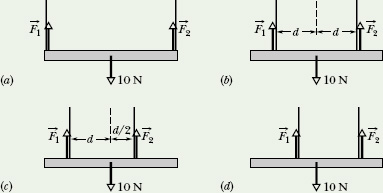
CHECKPOINT 5   A horizontal uniform bar of weight 10 N is to hang from a ceiling by two wires that exert upward forces  and  on the bar. The figure shows four arrangements for the wires. Which arrangements, if any, are indeterminate (so that we cannot solve for numerical values of  and )?