Equilibrium

Consider these objects: (1) a app resting on a table, (2) a hockey puck sliding with constant velocity across a frictionless surface, (3) the rotating blades of a ceiling fan, and (4) the wheel of a bicycle that is traveling along a straight path at constant speed. For each of these four objects,

1. The linear momentum  of its center of mass is constant.

2. Its angular momentum  about its center of mass, or about any other point, is also constant.

We say that such objects are in equilibrium. The two requirements for equilibrium are then

Our concern in this lesson is with situations in which the constants in Eq. 12-1 are zero; that is, we are concerned largely with objects that are not moving in any way—either in translation or in rotation—in the reference frame from which we observe them. Such objects are in static equilibrium. Of the four objects mentioned at the beginning of this section, only one—the app resting on the table—is in static equilibrium.

The balancing rock of Fig. 12-1 is another example of an object that, for the present at least, is in static equilibrium. It shares this property with countless other structures, such as cathedrals, houses, filing cabinets, and taco stands, that remain stationary over time.

As we discussed in Section 8-6, if a body returns to a state of static equilibrium after having been displaced from that state by a force, the body is said to be in stable static equilibrium. A marble placed at the bottom of a hemispherical bowl is an example. However, if a small force can displace the body and end the equilibrium, the body is in unstable static equilibrium.

For example, suppose we balance a domino with the domino’s center of mass vertically above the supporting edge, as in Fig. 12-2a. The torque about the supporting edge due to the gravitational force  on the domino is zero because the line of action of  is through that edge. Thus, the domino is in equilibrium. Of course, even a slight force on it due to some chance disturbance ends the equilibrium. As the line of action of  moves to one side of the supporting edge (as in Fig. 12-2b), the torque due to  increases the rotation of the domino. Therefore, the domino in Fig. 12-2a is in unstable static equilibrium.

The domino in Fig. 12-2c is not quite as unstable. To topple this domino, a force would have to rotate it through and then beyond the balance position of Fig. 12-2a, in which the center of mass is above a supporting edge. A slight force will not topple this domino, but a vigorous flick of the finger against the domino certainly will. (If we arrange a chain of such upright dominos, a finger flick against the first can cause the whole chain to fall.)

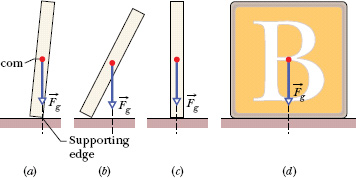
Fig. 12-2   (a) A domino balanced on one edge, with its center of mass vertically above that edge. The gravitational force  on the domino is directed through the supporting edge. (b) If the domino is rotated even slightly from the balanced orientation, then  causes a torque that increases the rotation. (c) A domino upright on a narrow side is somewhat more stable than the domino in (a). (d) A square block is even more stable.

The child’s square block in Fig. 12-2d is even more stable because its center of mass would have to be moved even farther to get it to pass above a supporting edge. A flick of the finger may not topple the block. (This is why you never see a chain of toppling square blocks.) The worker in Fig. 12-3 is like both the domino and the square block: Parallel to the beam, his stance is wide and he is stable; perpendicular to the beam, his stance is narrow and he is unstable (and at the mercy of a chance gust of wind).

The analysis of static equilibrium is very important in engineering practice. The design engineer must isolate and identify all the external forces and torques that may act on a structure and, by good design and wise choice of materials, ensure that the structure will remain stable under these loads. Such analysis is necessary to ensure, for example, that bridges do not collapse under their traffic and wind loads and that the landing gear of aircraft will function after the shock of rough landings.

Fig. 12-3   A construction worker balanced on a steel beam is in static equilibrium but is more stable parallel to the beam than perpendicular to it.