A simple gyroscope consists of a wheel fixed to a shaft and free to spin about the axis of the shaft. If one end of the shaft of a nonspinning gyroscope is placed on a support as in Fig. 11-22a and the gyroscope is released, the gyroscope falls by rotating downward about the tip of the support. Since the fall involves rotation, it is governed by Newton’s second law in angular form, which is given by Eq. 11-29:

This equation tells us that the torque causing the downward rotation (the fall) changes the angular momentum ![]() of the gyroscope from its initial value of zero. The torque
of the gyroscope from its initial value of zero. The torque ![]() is due to the gravitational force
is due to the gravitational force ![]() acting at the gyroscope’s center of mass, which we take to be at the center of the wheel. The moment arm relative to the support tip, located at O in Fig. 11-22a, is
acting at the gyroscope’s center of mass, which we take to be at the center of the wheel. The moment arm relative to the support tip, located at O in Fig. 11-22a, is ![]() . The magnitude of
. The magnitude of ![]() is
is
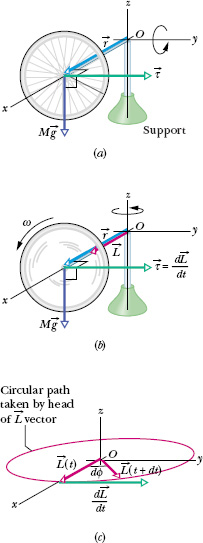
Fig. 11-22 (a) A nonspinning gyroscope falls by rotating in an xz plane because of torque ![]() . (b) A rapidly spinning gyroscope, with angular momentum
. (b) A rapidly spinning gyroscope, with angular momentum ![]() , precesses around the z axis. Its precessional motion is in the xy plane. (c) The change
, precesses around the z axis. Its precessional motion is in the xy plane. (c) The change ![]() in angular momentum leads to a rotation of
in angular momentum leads to a rotation of ![]() about O.
about O.

(because the angle between ![]() and
and ![]() is 90°), and its direction is as shown in Fig. 11-22a.
is 90°), and its direction is as shown in Fig. 11-22a.
A rapidly spinning gyroscope behaves differently. Assume it is released with the shaft angled slightly upward. It first rotates slightly downward but then, while it is still spinning about its shaft, it begins to rotate horizontally about a vertical axis through support point O in a motion called precession.
Why does the spinning gyroscope stay aloft instead of falling over like the nonspinning gyroscope? The clue is that when the spinning gyroscope is released, the torque due to ![]() must change not an initial angular momentum of zero but rather some already existing nonzero angular momentum due to the spin.
must change not an initial angular momentum of zero but rather some already existing nonzero angular momentum due to the spin.
To see how this nonzero initial angular momentum leads to precession, we first consider the angular momentum ![]() of the gyroscope due to its spin. To simplify the situation, we assume the spin rate is so rapid that the angular momentum due to precession is negligible relative to
of the gyroscope due to its spin. To simplify the situation, we assume the spin rate is so rapid that the angular momentum due to precession is negligible relative to ![]() . We also assume the shaft is horizontal when precession begins, as in Fig. 11-22b. The magnitude of
. We also assume the shaft is horizontal when precession begins, as in Fig. 11-22b. The magnitude of ![]() is given by Eq. 11-31:
is given by Eq. 11-31:

where I is the rotational moment of the gyroscope about its shaft and ω is the angular speed at which the wheel spins about the shaft. The vector ![]() points along the shaft, as in Fig. 11-22b. Since
points along the shaft, as in Fig. 11-22b. Since ![]() is parallel to
is parallel to ![]() , torque
, torque ![]() must be perpendicular to
must be perpendicular to ![]() .
.
According to Eq. 11-41, torque ![]() causes an incremental change
causes an incremental change ![]() in the angular momentum of the gyroscope in an incremental time interval dt; that is,
in the angular momentum of the gyroscope in an incremental time interval dt; that is,

However, for a rapidly spinning gyroscope, the magnitude of ![]() is fixed by Eq. 11-43. Thus the torque can change only the direction of
is fixed by Eq. 11-43. Thus the torque can change only the direction of ![]() , not its magnitude.
, not its magnitude.
From Eq. 11-44 we see that the direction of ![]() is in the direction of
is in the direction of ![]() , perpendicular to
, perpendicular to ![]() . The only way that
. The only way that ![]() can be changed in the direction of
can be changed in the direction of ![]() without the magnitude L being changed is for
without the magnitude L being changed is for ![]() to rotate around the z axis as shown in Fig. 11-22c.
to rotate around the z axis as shown in Fig. 11-22c. ![]() maintains its magnitude, the head of the
maintains its magnitude, the head of the ![]() vector follows a circular path, and
vector follows a circular path, and ![]() is always tangent to that path. Since
is always tangent to that path. Since ![]() must always point along the shaft, the shaft must rotate about the z axis in the direction of
must always point along the shaft, the shaft must rotate about the z axis in the direction of ![]() . Thus we have precession. Because the spinning gyroscope must obey Newton’s law in angular form in response to any change in its initial angular momentum, it must precess instead of merely toppling over.
. Thus we have precession. Because the spinning gyroscope must obey Newton’s law in angular form in response to any change in its initial angular momentum, it must precess instead of merely toppling over.
We can find the precession rate Ω by first using Eqs. 11-44 and 11-42 to get the magnitude of ![]() :
:

As ![]() changes by an incremental amount in an incremental time interval dt, the shaft and
changes by an incremental amount in an incremental time interval dt, the shaft and ![]() precess around the z axis through incremental angle d
precess around the z axis through incremental angle d![]() . (In Fig. 11-22c, angle d
. (In Fig. 11-22c, angle d![]() is exaggerated for clarity.) With the aid of Eqs. 11-43 and 11-45, we find that d
is exaggerated for clarity.) With the aid of Eqs. 11-43 and 11-45, we find that d![]() is given by
is given by
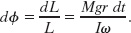
Dividing this expression by dt and setting the rate Ω = d![]() /dt, we obtain
/dt, we obtain

This result is valid under the assumption that the spin rate ω is rapid. Note that Ω decreases as ω is increased. Note also that there would be no precession if the gravitational force ![]() did not act on the gyroscope, but because I is a function of M, mass cancels from Eq. 11-46; thus Ω is independent of the mass.
did not act on the gyroscope, but because I is a function of M, mass cancels from Eq. 11-46; thus Ω is independent of the mass.
Equation 11-46 also applies if the shaft of a spinning gyroscope is at an angle to the horizontal. It holds as well for a spinning top, which is essentially a spinning gyroscope at an angle to the horizontal.
Leave a Reply