E1–E2–E1cB Spectrum

We can also compare these with the other elimination reactions by thinking of the relative timing of proton removal and leaving group departure. E1 is at one end of the scale: the leaving group goes first, and proton removal follows in a second step. In E2 reactions, the two events happen at the same time: the proton is removed as the leaving group leaves. In E1cB the proton removal moves in front of leaving group departure.

The correlation of many features of β-elimination reactions is greatly aided by recognition that these three mechanisms represent variants of a continuum of mechanistic possibilities. Many β-eliminations occur via mechanisms that are intermediate between the limiting mechanistic types. This idea, called the variable E2 transition state theory, is outlined as below.

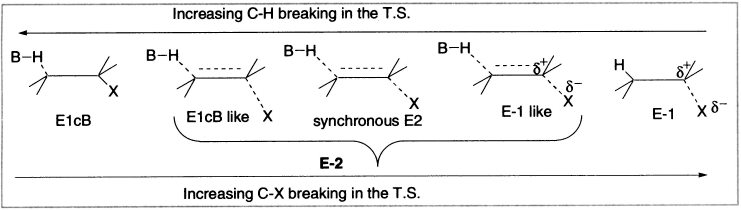
Figure 4.7 Variable transition state theory of elimination reactions

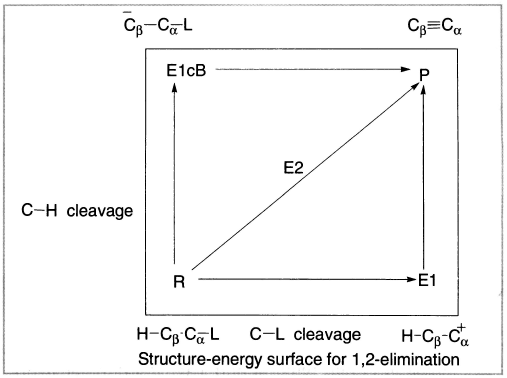
Figure 4.8 More O’ Ferral–Jencks diagram

Figure 4.8 is a two-dimensional projection of a three-dimensional potential energy surface for a reaction. Because of the high energy of both the E1 and E1cB intermediates, the lowest energy path will be a concerted E2 path, more or less diagonally across the energy surface. This pathway is of lower energy, because the partially formed double bond provides some compensation for the energy required to break the C-H and C-X bonds, and the high-energy intermediates are avoided.

In the three mechanisms so far considered, the similarities are greater than the differences. In each case, there is a leaving group that comes off with its pair of electrons and another group (usually H) that comes off without them. The only differences are in the order of the steps.

There is a spectrum of mechanisms ranging from one extreme, in which the leaving group departs well before the proton (Pure E1), to the other extreme, in which the proton comes off first and then, after some time, the leaving group follows (Pure E1cB). The pure E2 case would be somewhere in the middle, with both groups leaving simultaneously. However, most E2 reactions are not exactly in the middle, but somewhere to one side or the other.

Where a given reaction stands on the above spectrum can be expressed with the help of the transition state, depending on which bond (C-H) or (C-X) has undergone more cleavage.

One way to determine this is to study isotope effects, which ought to tell us something about the behaviour of bonds in the transition state; for example, CH₃CH₂N⁺Me₃ showed a nitrogen isotope effect (K¹⁴/K¹⁵) of 1.017, while PhCH₂CH₂N⁺Me₃ gave a corresponding value of 1.009. It would be expected that the phenyl group would move the reaction forward to the E1cB side of the line, which means that for this compound, the C–N bond is not as greatly broken in the transition state as it is for the unsubstituted one. The isotope effect shows that in the phenyl compound, the mass of the nitrogen has less effect on the reaction rate than it does in the unsubstituted compound. Similar results have been obtained with S⁺R₂ leaving groups by the use of ³²S/³⁴S isotope effects and with Cl (³⁵C1/³⁷Cl). Other isotope effects/studies have involved labelled α or β carbon, labelled a hydrogen, or labelled base.

Another way to study the position of a given reaction on the spectrum involves the use of β-aryl substitution. Since a positive Hammet ρ value is an indication of a negatively charged transition state, the ρ value for substituted β-aryl groups should increase, as a reaction moves from being E1-like to E1cB-like along the spectrum; for example, ρ values of ArCH₂CH₂X increase as the leaving group’s ability of X decreases.

ρ value for X= I, 2.07; Br, 2.14; Cl, 2.61; S⁺Me₂, 2.75; F, 3.12.

To conclude, some points may be summarized:

• Methyl halides cannot eliminate, as there are no appropriately placed protons.
• Increasing branching favours elimination over substitution, and strongly basic, hindered nucleophiles always eliminate unless there is no option.
• A good nucleophile may not necessarily be a good base or vice versa. Good nucleophiles undergo substitution by S_N2 unless the substrate is tertiary, and then the intermediate cation can eliminate by E1 as well as substitute by S_N1. On increasing the concentration and strength of a base, the unimolecular reaction tends to bimolecularity. This change in bimolecularity is more pronounced in E1 than in S_N1 reactions.
• High temperatures favour elimination by gearing up the importance of entropy in the free energy of reaction; consequently, the E/S_N ratio also increases.
• A less polar solvent not only favours bimolecular reactions, but also the E2 reaction to the S_N2 reaction.