In 1965 R.B. Woodward, an experimentalist, and Ronald Hoffmann, a theorist, developed the conservation of orbital symmetry theory to explain electrocyclic reactions. This theory explains the relationship among the structure and configuration of the reactant, the conditions (thermal and /or photochemical) under which the reaction takes place and the configuration of the product.
The overlap of p orbitals to form π bonds can be described mathematically using quantum mechanics. The result of the mathematical treatment can be described simply in nonmathematical terms using molecular orbital theory put forth by Kenichi Fukui.
- The two lobes of p orbital are of opposite phase. When two in-phase atomic orbitals overlap, a covalent bond is formed. When two out-of-phase atomic orbitals overlap, a node is created between the two nuclei. A node is a region in which there is zero probability of finding an electron.
- Electrons fill molecular orbitals according to the same rules that are used when they fill atomic orbitals: an electron goes into the available molecular orbital with the lowest energy, and only two electrons can occupy a molecular orbital.
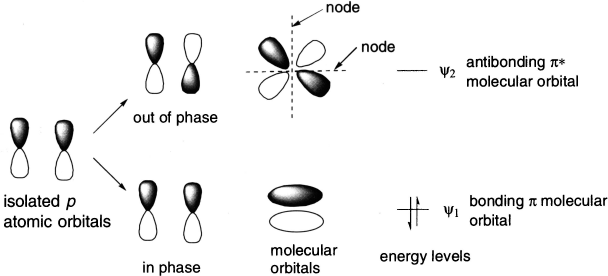
Since the π-bonding portion of a molecule is perpendicular to the framework of the σ bonds, the π-bonds can be treated independently. Each carbon atom that forms a π-bond has a p orbital, and p orbitals of the carbon atoms combine to produce a π molecular orbital that is described by the linear combination of atomic orbitals (LCAO).
Ethene has only one π bond, but it has two p atomic orbitals that combine to produce two π molecular orbitals, that is, lower energy bonding π molecular orbital, designated by ψ1 and higher energy antibonding π* molecular orbital, ψ2. The bonding molecular orbital results from additive overlap of the atomic orbitals, whereas the antibonding molecular orbital results from subtractive overlap.
1,3-Butadiene has two conjugated bonds; it has four p atomic orbitals that can combine linearly in four different ways to give four π molecular orbitals: ψ1, ψ2, ψ3 and ψ4. Notice that orbitals are conserved: two atomic orbitals combine to produce two molecular orbitals; four atomic orbitals combine to produce four molecular orbitals; six atomic orbitals combine to produce six molecular orbitals.
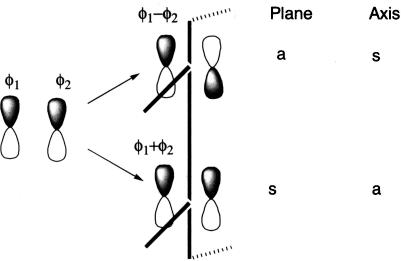
Let us first define the symmetry properties of a 1s and a 2p orbital with respect to a plane of symmetry or an axis of symmetry. Imagine holding a mirror perpendicular to the plane of the paper along the centre of the molecular orbital. If the left half of the molecular orbital is the mirror image of the right half, the molecular orbital is symmetric. If it is not, it is antisymmetric. The easier way to know whether a molecular orbital is symmetric or antisymmetric to plane is: if the p orbitals at the ends of the molecular orbitals are identical, the molecular orbital is symmetric and if they are not identical, the molecular orbital is asymmetric.
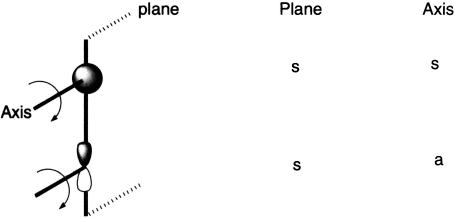
One can take this one step further by considering the symmetry properties of molecular orbitals formed by the overlap of two or more atomic orbitals. Molecular orbitals formed from two overlapping sigma orbitals:
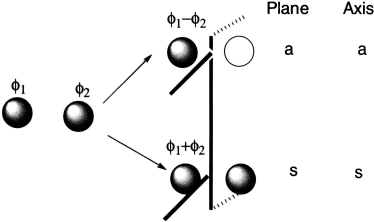
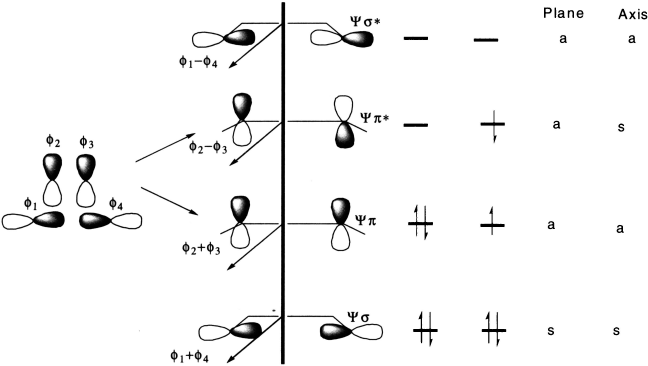
Molecular orbitals formed from two overlapping p orbitals (sigma bonds):
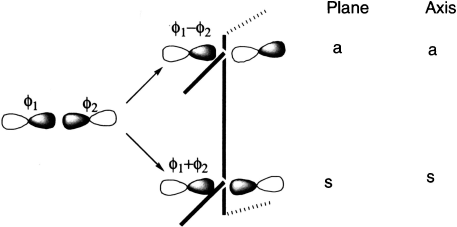
Molecular orbitals formed from two parallel overlapping p orbitals (π bonds):
We can now use these basic orbitals to construct the relevant molecular orbitals for two interconverting molecules, cyclobutene and butadiene. Note particularly that we need only construct the molecular orbitals explicitly involved in the reaction; most of the sigma framework remains unchanged and no orbitals derived from this need to be considered.
In order to interconvert cyclobutene and butadiene, the four molecular orbitals labelled ψ1, ψ2, ψ3, ψ4 must be converted into ψσ, ψπ, ψπ*, ψσ*. There are two stereochemically distinct ways in which this might be accomplished.
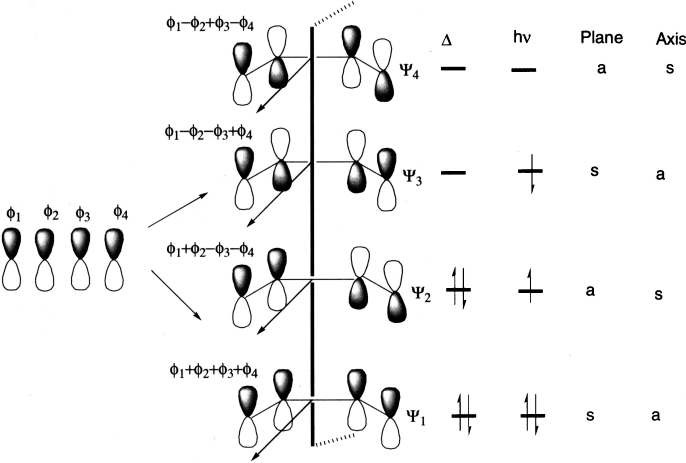
A molecular orbital is bonding if the number of bonding interactions is greater than the number of nodes between the nuclei, and the molecular orbital is antibonding if the number of bonding interactions is fewer than the number of nodes between the nuclei. The normal electronic configuration of a molecule is known as its ground state. If a molecule absorbs light of an appropriate wavelength an electron from its ground state HOMO (ψ2) will be promoted to its excited state LUMO (ψ3). In the excited state, the HOMO is ψ3 and LUMO is ψ4.
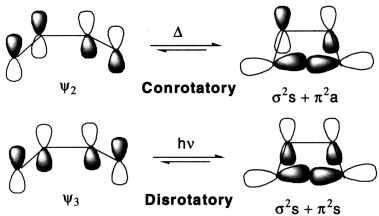
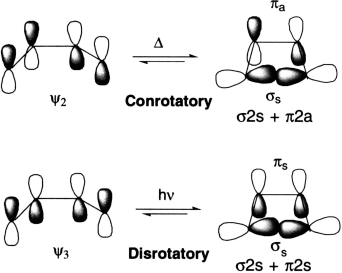
The product of an electrocyclic reaction is formed as a result of formation of a new σ bond. In order to form this bond, the p-orbitals at the end of the conjugated system must rotate so they can overlap head-to-head (and rehybridize to sp3). Rotation can occur in two ways. If both orbitals rotate in the same direction (both clockwise or both anti clockwise), ring closure is conrotatory. If the orbitals rotate in opposite directions, ring closure is disrotatory.
The 4π-electrons of butadiene are accommodated in the two bonding molecular orbitals, ψ1 and ψ2 so that ψ2 is the HOMO. It is quite evident that overlap of the terminal π-lobes of the same phase, forming a σ-bond is possible only by a conrotatory motion (rotation of 90° of two terminal bonds in the same direction). A disrotatory motion in the HOMO, on the other hand, leads to an antibonding interaction (σ*). In thermal electrocyclic reactions of a 4π-electron system, therefore, only conrotatory motion is allowed and the stereochemistry follows accordingly. On photoexcitation of butadiene, one of the π-electrons is transferred to ψ3 that becomes the HOMO. An inspection of the molecular orbital shows that a disrotatory motion leads to an overlap of the terminal π-lobes of the same phase and a different stereochemistry follows.
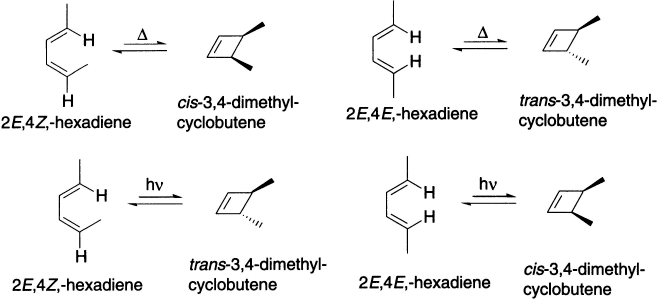
Under thermal conditions, 2E,4Z-hexadiene cyclizes to cis-3,4-dimethyl-cyclobutene, and 2E,4E-hexadiene cyclizes to trans-3,4-dimethyl-cyclobutene. When the reactions are carried out under photochemical conditions, the configuration of the product changes that is, the trans isomer is obtained instead of the cis isomer and the cis isomer is obtained instead of the trans isomer.
Some notations, which are used in cycloaddition reactions, may be defined here to indicate the mode of additions. If a component undergoes addition on the same face, it is called suprafacial component, whereas if a component undergoes addition on opposite faces, it is called an antarafacial component. The two modes of addition are known as suprafacial and antarafacial, respectively. Accordingly, conrotation involves an antarafacial and disrotation a suprafacial interaction between the two termini of the reacting species in electrocyclic reactions.
In a thermal conrotatory ring opening of cyclobutene, the σ-HOMO of the σ-component interacts with the π-LUMO of the π-component with in-phase overlap, the former behaving as a suprafacial component and the latter as an antarafacial one. The reaction is designated [σ2s + π2a]. Alternatively, the same reaction may be considered in terms of interaction between the σ-LUMO, that is, σ* and the π-HOMO, that is, π and thus designated [σ2a + π2s]. Similarly, the disrotatory photochemical ring opening of cyclobutene, in which the σ-HOMO interacts suprafacially with the π-LUMO*, is designated [σ2s + π2s]. Alternatively, if the interaction between the σ-LUMO and the π-HOMO is considered, it may be designated [σ2a + σ2a].
A symmetry-allowed pathway leads to overlap of in-phase orbitals; a symmetry-forbidden pathway leads to overlap of out-of-phase orbitals. Symmetry-allowed reaction could take place under relatively mild conditions. If a reaction is symmetry-forbidden, it cannot take place by concerted pathway.
Opening of the cyclopropyl cation involves only one electron arrow and, hence, the number of cyclically conjugated electrons is 2 (4n+2, n=0). Under thermal conditions, this will go via a Huckel topology involving suprafacial components, which has the effect of rotating both methyl groups outwards in opposite directions (disrotation).

Whilst this rule is normally followed fairly well for ground states, it can be overturned when, for example, steric or geometrical strain in the ‘allowed’ pathway promotes the ‘forbidden’ route. The situation is actually more complex for photochemical reactions, and much recent evidence suggests that the Woodward-Hoffmann rules are not always followed.
Thus a ‘suprafacial’ or ‘Huckel’ transition state in a pericyclic reaction is particularly favourable if the number of cyclically conjugated π electrons in the transition state equals 4n+2 (the Huckel rule, where n = 0, 1, 2, etc).
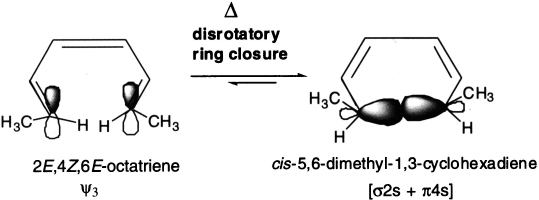
The treatment is extended to 1,3,5-hexatriene–cyclohexadiene interconversion. The ground state HOMO (ψ3) of a compound with three conjugated π-bonds, such as (2E,4Z,6E)-octatriene, is symmetric. This means that ring closure under thermal conditions is disrotatory. In disrotatory ring closure of (2E,4Z,6E)-octatriene, the methyl groups are both pushed up (or down) resulting in the formation of a cis product.
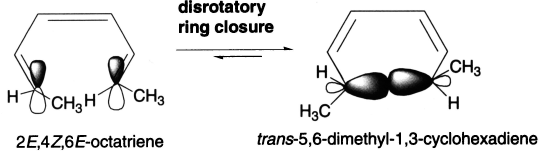
In disrotatory ring closure of (2E,4Z,6Z)-octatriene, the one methyl group is pushed up and the other is pushed down resulting in the formation of a trans product.
If the reaction takes place under photochemical conditions, we must consider the excited state HOMO rather than the ground state HOMO. The excited state HOMO (ψ4) of a compound with three π-bonds is asymmetric. Therefore, under photochemical conditions, (2E,4Z,6Z)-octatriene undergoes conrotatory ring closure, so both methyl groups are pushed down (or up) and the cis product is formed.
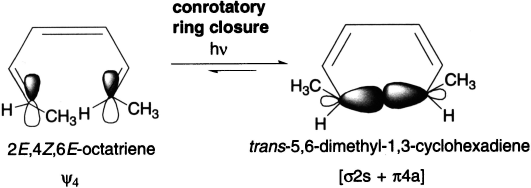
Thus, symmetry of the HOMO of the compound undergoing ring closure controls the outcome of an electrocyclic reaction. Ring closure of (2E,4Z)-hexadiene forms cis-3,4-dimethylcyclobutene. The compound undergoing ring closure has two conjugated π-bonds. The ground state HOMO of a compound with two conjugated π-bonds is asymmetric, so ring closure is conrotatory. Conrotatory ring closure of (2E,4Z)-hexadiene leads to the cis product.
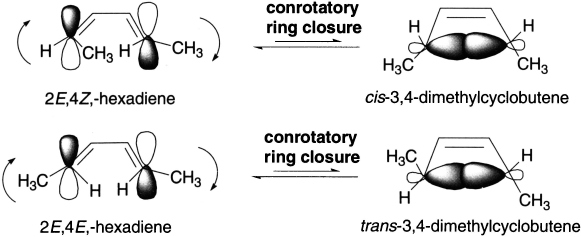
However, if the reaction is carried out under photochemical conditions, the excited state HOMO of a compound with two conjugated π-bonds is symmetric. So 2E,4Z-hexadiene will undergo disrotatory ring closure, resulting in the trans product, while 2E,4E-hexadiene will undergo disrotatory ring closure and form the cis product.
We have seen that the HOMO of a compound with two conjugated double bonds is asymmetric, whereas the HOMO of a compound with three conjugated double bonds is symmetric. If we examine molecular orbital diagrams for compounds with four, five, six and more conjugated double bonds, we can conclude that the ground state HOMO of a compound with an even number of conjugated double bonds is asymmetric, whereas the ground-state HOMO of a compound with an odd number of conjugated double bonds is symmetric. Therefore, from the number of conjugated double bonds in a compound, we can immediately tell whether ring closure will be conrotatory (an even number of conjugated double bonds) or disrotatory (an odd number of conjugated double bonds) under thermal conditions. However, if the reaction takes place under photochemical conditions, everything is reversed, because the ground-state and excited-state HOMOs have opposite symmetries.
We have seen that the stereochemistry of an electrocyclic reaction depends on the mode of ring closure. In turn, the mode of ring closure depends on the number of conjugated π bonds in the reactant and on whether the reaction is carried out under thermal or photochemical conditions. What we have learned about pericyclic reactions can be summarized with a series of selection rules. These are also known as the Woodward–Hoffmann rules for electrocyclic reactions.
Table 11.1 Woodward–Hoffmann Rules for Electrocyclic Reactions
| No. of conjugated π bond | Reaction conditions | Allowed mode of ring closure |
|---|---|---|
| Even number | Thermal Photochemical | Conrotatory Disrotatory |
| Odd number | Thermal Photochemical | Disrotatory Conrotatory |
The following series of reactions illustrate just how easy it is to determine the mode of ring closure and, therefore, the product of an electrocyclic reaction. The reactant of the first reaction has three conjugate double bonds and is undergoing ring closure under thermal conditions. Ring closure is therefore disrotatory. Disrotatory ring closure of this reactant causes the hydrogens to be cis in the ring-closed product.
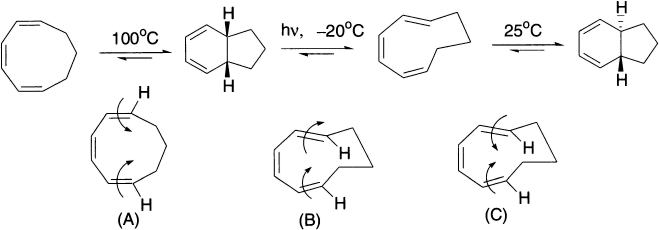
The second step is a ring-opening electrocyclic reaction that takes place under photochemical conditions. Because of the principle of microscopic reversibility, the orbital symmetry rules used for a ring-closure reaction also apply to the reverse ring-opening reaction. Because the reaction occurs under photochemical conditions, ring opening (or ring closure) is conrotatory. In order for conrotatory rotation to result in a product with cis hydrogens, the hydrogens in the compound undergoing ring closure must point in the same direction. The third step is a thermal ring closure of a compound with three conjugated double bonds, so ring closure is disrotatory. Drawing the hydrogens and the arrows allows us to determine the configurations of the hydrogens in the ring-closed product.
Huckel was also able to show that if a cyclic conjugated π system is irradiated with light so that it goes into the first ‘excited’ electronic state, it is especially stable if the number of cyclically conjugated electrons equal 4n. Hence, photochemically activated pericyclic reactions will proceed suprafacially via a Huckel transition state if the electron count corresponds to 4n. The antarafacial mode described above has no counterpart in a stable aromatic molecule, as benzene did for the suprafacial mode. An antarafacial mode could be formed by taking benzene and giving the π system a 180° twist. If this is done, the resultant ‘twisted’ benzene has been termed ‘Mobius Benzene.’
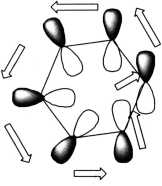
Here the electron density continuity passes through the plane of the molecule, from the top face through to the bottom face. Such a MOBIUS system it turns out is especially stable if it contains 4n electrons (or 4n+2 if photochemically excited). These four conditions are most easily summarized as follows:
- A thermally activated pericyclic reaction will proceed via a Huckel topology containing only suprafacial components if the cyclically conjugated π electrons equal 4n+2 (n=0,1,2 etc).
- A photochemically activated pericyclic reaction may proceed via a Huckel topology containing only suprafacial components if the cyclically conjugated π electrons equal 4n.
- A thermally activated pericyclic reaction will proceed via a Mobius topology containing ONE antarafacial component if the cyclically conjugated π electrons equal 4n (n = 0,1,2 etc).
- A photochemically activated pericyclic reaction may proceed via a Mobius topology containing ONE antarafacial component if the cyclically conjugated π electrons equal 4n+2 (n = 0,1,2 etc).
It would be a good point here to remind you that, although all electrocyclic reactions are allowed both thermally and photochemically, providing the reaction is right, the steric requirements for conrotatory or disrotatory cyclization or ring opening may make one or both modes impossible.
Leave a Reply