We have discussed the transfer of energy as heat between a system and its environment, but we have not yet described how that transfer takes place. There are three transfer mechanisms: conduction, convection, and radiation.
Conduction
If you leave the end of a metal poker in a fire for enough time, its handle will get hot. Energy is transferred from the fire to the handle by (thermal) conduction along the length of the poker. The vibration amplitudes of the atoms and electrons of the metal at the fire end of the poker become relatively large because of the high temperature of their environment. These increased vibrational amplitudes, and thus the associated energy, are passed along the poker, from atom to atom, during collisions between adjacent atoms. In this way, a region of rising temperature extends itself along the poker to the handle.
Consider a slab of face area A and thickness L, whose faces are maintained at temperatures TH and TC by a hot reservoir and a cold reservoir, as in Fig. 18-18. Let Q be the energy that is transferred as heat through the slab, from its hot face to its cold face, in time t. Experiment shows that the conduction rate Pcond (the amount of energy transferred per unit time) is
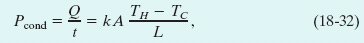
Fig. 18-18 Thermal conduction. Energy is transferred as heat from a reservoir at temperature TH to a cooler reservoir at temperature TC through a conducting slab of thickness L and thermal conductivity k.
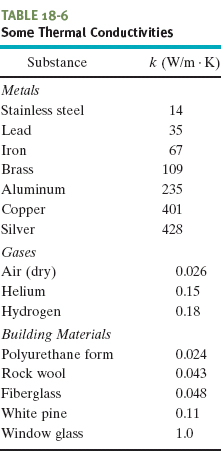
in which k, called the thermal conductivity, is a constant that depends on the material of which the slab is made. A material that readily transfers energy by conduction is a good thermal conductor and has a high value of k. Table 18-6 gives the thermal conductivities of some common metals, gases, and building materials.
Thermal Resistance to Conduction (R-Value)
If you are interested in insulating your house or in keeping cola cans cold on a picnic, you are more concerned with poor heat conductors than with good ones. For this reason, the concept of thermal resistance R has been introduced into engineering practice. The R-value of a slab of thickness L is defined as

The lower the thermal conductivity of the material of which a slab is made, the higher the R-value of the slab; so something that has a high R-value is a poor thermal conductor and thus a good thermal insulator.
Note that R is a property attributed to a slab of a specified thickness, not to a material. The commonly used unit for R (which, in the United States at least, is almost never stated) is the square foot–Fahrenheit degree–hour per British thermal unit (ft2 · F° · h/Btu). (Now you know why the unit is rarely stated.)
Conduction Through a Composite Slab
Figure 18-19 shows a composite slab, consisting of two materials having different thicknesses L1 and L2 and different thermal conductivities k1 and k2. The temperatures of the outer surfaces of the slab are TH and TC. Each face of the slab has area A. Let us derive an expression for the conduction rate through the slab under the assumption that the transfer is a steady-state process; that is, the temperatures everywhere in the slab and the rate of energy transfer do not change with time.
In the steady state, the conduction rates through the two materials must be equal. This is the same as saying that the energy transferred through one material in a certain time must be equal to that transferred through the other material in the same time. If this were not true, temperatures in the slab would be changing and we would not have a steady-state situation. Letting TX be the temperature of the interface between the two materials, we can now use Eq. 18-32 to write
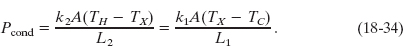
Solving Eq. 18-34 for TX yields, after a little algebra,
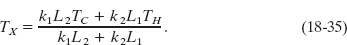
Substituting this expression for TX into either equality of Eq. 18-34 yields
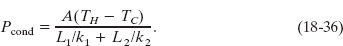
We can extend Eq. 18-36 to apply to any number n of materials making up a slab:

The summation sign in the denominator tells us to add the values of L/k for all the materials.
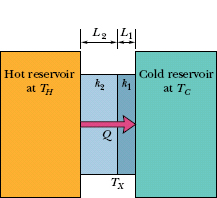
Fig. 18-19 Heat is transferred at a steady rate through a composite slab made up of two different materials with different thicknesses and different thermal conductivities. The steady-state temperature at the interface of the two materials is TX.
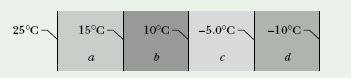
CHECKPOINT 7 The figure shows the face and interface temperatures of a composite slab consisting of four materials, of identical thicknesses, through which the heat transfer is steady. Rank the materials according to their thermal conductivities, greatest first.
Convection
When you look at the flame of a candle or a match, you are watching thermal energy being transported upward by convection. Such energy transfer occurs when a fluid, such as air or water, comes in contact with an object whose temperature is higher than that of the fluid. The temperature of the part of the fluid that is in contact with the hot object increases, and (in most cases) that fluid expands and thus becomes less dense. Because this expanded fluid is now lighter than the surrounding cooler fluid, buoyant forces cause it to rise. Some of the surrounding cooler fluid then flows so as to take the place of the rising warmer fluid, and the process can then continue.
Convection is part of many natural processes. Atmospheric convection plays a fundamental role in determining global climate patterns and daily weather variations. Glider pilots and birds alike seek rising thermals (convection currents of warm air) that keep them aloft. Huge energy transfers take place within the oceans by the same process. Finally, energy is transported to the surface of the Sun from the nuclear furnace at its core by enormous cells of convection, in which hot gas rises to the surface along the cell core and cooler gas around the core descends below the surface.
Radiation
The third method by which an object and its environment can exchange energy as heat is via electromagnetic waves (visible light is one kind of electromagnetic wave). Energy transferred in this way is often called thermal radiation to distinguish it from electromagnetic signals (as in, say, television broadcasts) and from nuclear radiation (energy and particles emitted by nuclei). (To “radiate” generally means to emit.) When you stand in front of a big fire, you are warmed by absorbing thermal radiation from the fire; that is, your thermal energy increases as the fire’s thermal energy decreases. No medium is required for heat transfer via radiation—the radiation can travel through vacuum from, say, the Sun to you.
The rate Prad at which an object emits energy via electromagnetic radiation depends on the object’s surface area A and the temperature T of that area in kelvins and is given by

Here σ = 5.6703 × 10−8 W/m2 · K4 is called the Stefan–Boltzmann constant after Josef Stefan (who discovered Eq. 18-38 experimentally in 1879) and Ludwig Boltzmann (who derived it theoretically soon after). The symbol ε represents the emissivity of the object’s surface, which has a value between 0 and 1, depending on the composition of the surface. A surface with the maximum emissivity of 1.0 is said to be a blackbody radiator, but such a surface is an ideal limit and does not occur in nature. Note again that the temperature in Eq. 18-38 must be in kelvins so that a temperature of absolute zero corresponds to no radiation. Note also that every object whose temperature is above 0 K—including you—emits thermal radiation. (See Fig. 18-20.)

Fig. 18-20 A false-color thermo-gram reveals the rate at which energy is radiated by a house. The rates, from largest to smallest, are color-coded as white, yellow, red, purple, green, and black. You can tell that the roof and windows are poorly insulated.
The rate Pabs at which an object absorbs energy via thermal radiation from its environment, which we take to be at uniform temperature Tenv (in kelvins), is

The emissivity ε in Eq. 18-39 is the same as that in Eq. 18-38. An idealized blackbody radiator, with ε = 1, will absorb all the radiated energy it intercepts (rather than sending a portion back away from itself through reflection or scattering).
Because an object will radiate energy to the environment while it absorbs energy from the environment, the object’s net rate Pnet of energy exchange due to thermal radiation is
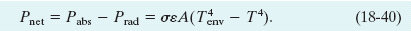
Pnet is positive if net energy is being absorbed via radiation and negative if it is being lost via radiation.
Thermal radiation is involved in the numerous cases of a dead rattlesnake striking a hand reaching toward it, as discussed in the opening story of this lesson. Pits between each eye and nostril of a rattlesnake serve as sensors of thermal radiation (note them in this lesson’s opening photograph). When, say, a mouse moves close to a rattlesnake’s head, the thermal radiation from the mouse triggers these sensors, causing a reflex action in which the snake strikes the mouse with its fangs and injects its venom. The thermal radiation from a reaching hand can cause the same reflex action even if the snake has been dead for a while because the snake’s nervous system continues to function. As one snake expert advised, if you must remove a recently killed rattlesnake, use a long stick rather than your hand.
Figure 18-21 shows the cross section of a wall made of white pine of thickness La and brick of thickness Ld (= 2.0La), sandwiching two layers of unknown material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is ka and that of the brick is kd (= 5.0ka). The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state; the only known interface temperatures are T1 = 25°C, T2 = 20°C, and T5 =−10°C. What is interface temperature T4?
Solution: One Key Idea here is that temperature T4 helps determine the rate Pd at which energy is conducted through the brick, as given by Eq. 18-32. However, we lack enough data to solve Eq. 18-32 for T4. A second Key Idea is that because the conduction is steady, the conduction rate Pd through the brick must equal the conduction rate Pa through the pine. From Eq. 18-32 and Fig. 18-21, we can write
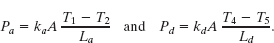
Setting Pa = Pd and solving for T4 yield
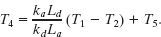
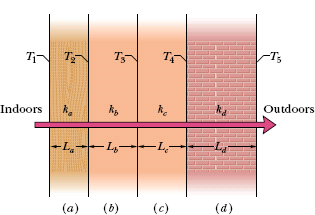
Fig. 18-21 A wall of four layers through which there is steady-state heat transfer.
Letting Ld = 2.0La and kd = 5.0ka, and inserting the known temperatures, we find
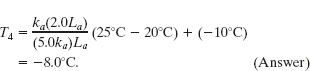
During an extended wilderness hike, you have a terrific craving for ice. Unfortunately, the air temperature drops to only 6.0°C each night—too high to freeze water. However, because a clear, moonless night sky acts like a blackbody radiator at a temperature of Ts = −23°C, perhaps you can make ice by letting a shallow layer of water radiate energy to such a sky. To start, you thermally insulate a container from the ground by placing a poorly conducting layer of, say, foam rubber or straw beneath it. Then you pour water into the container, forming a thin, uniform layer with mass m = 4.5 g, top surface area A = 9.0 cm2, depth d = 5.0 mm, emissivity ε = 0.90, and initial temperature 6.0°C. Find the time required for the water to freeze via radiation. Can the freezing be accomplished during one night?
Solution: One Key Idea is that the water cannot freeze at a temperature above the freezing point. Therefore, the radiation must first reduce the water temperature from 6.0°C to the freezing point of 0°C. Using Eq. 18-14 and Table 18-3, we find the associated energy loss to be
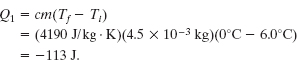
Thus, 113 J must be radiated away by the water to drop its temperature to the freezing point.
A second Key Idea is that the water must next have an additional energy loss Q2 for all of it to freeze. Using Eq. 18-16 (Q = mL) with the value of L being LF from Eq. 18-18 or Table 18-4, and inserting a minus sign to indicate an energy loss, we find
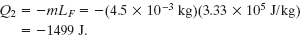
The total required energy loss is thus
Qtot = Q1 + Q2 = −113 J − 1499 J = −1612 J.
A third Key Idea is that, while the water loses energy by radiating to the sky, it also absorbs energy radiated to it from the sky. In a total time t, we want the net energy of this exchange to be the energy loss Qtot; so we want the power of this exchange to be
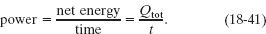
The power of such an energy exchange is also the net rate Pnet of thermal radiation, as given by Eq. 18-40; so the time t required for the energy loss to be Qtot is
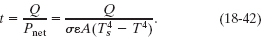
Although the temperature T of the water decreases slightly while the water is cooling, we can approximate T as being the freezing point, 273 K. With Ts = 250 K, the denominator of Eq. 18-42 is
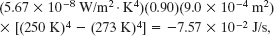
Because t is less than a night, freezing water by having it radiate to the dark sky is feasible. In fact, in some parts of the world people used this technique long before the introduction of electric freezers.
Leave a Reply