Here we look at four different thermodynamic processes, in each of which a certain restriction is imposed on the system. We then see what consequences follow when we apply the first law of thermodynamics to the process. The results are summarized in Table 18-5.
1. Adiabatic processes. An adiabatic process is one that occurs so rapidly or occurs in a system that is so well insulated that no transfer of energy as heat occurs between the system and its environment. Putting Q = 0 in the first law (Eq. 18-26) yields

This tells us that if work is done by the system (that is, if W is positive), the internal energy of the system decreases by the amount of work. Conversely, if work is done on the system (that is, if W is negative), the internal energy of the system increases by that amount.
Figure 18-15 shows an idealized adiabatic process. Heat cannot enter or leave the system because of the insulation. Thus, the only way energy can be transferred between the system and its environment is by work. If we remove shot from the piston and allow the gas to expand, the work done by the system (the gas) is positive and the internal energy of the gas decreases. If, instead, we add shot and compress the gas, the work done by the system is negative and the internal energy of the gas increases.

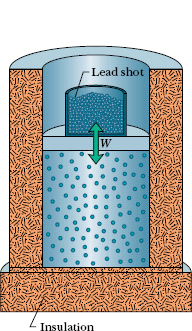
Fig. 18-15 An adiabatic expansion can be carried out by slowly removing lead shot from the top of the piston. Adding lead shot reverses the process at any stage.
2. Constant-volume processes. If the volume of a system (such as a gas) is held constant, that system can do no work. Putting W = 0 in the first law (Eq. 18-26) yields
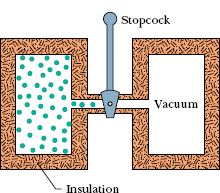
Fig. 18-16 The initial stage of a free-expansion process. After the stopcock is opened, the gas fills both chambers and eventually reaches an equilibrium state.
Thus, if heat is absorbed by a system (that is, if Q is positive), the internal energy of the system increases. Conversely, if heat is lost during the process (that is, if Q is negative), the internal energy of the system must decrease.
3. Cyclical processes. There are processes in which, after certain interchanges of heat and work, the system is restored to its initial state. In that case, no intrinsic property of the system—including its internal energy—can possibly change. Putting ΔEint = 0 in the first law (Eq. 18-26) yields
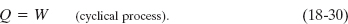
Thus, the net work done during the process must exactly equal the net amount of energy transferred as heat; the store of internal energy of the system remains unchanged. Cyclical processes form a closed loop on a p–V plot, as shown in Fig. 18-14f. We discuss such processes in detail in Lesson 20.
4. Free expansions. These are adiabatic processes in which no transfer of heat occurs between the system and its environment and no work is done on or by the system. Thus, Q = W = 0, and the first law requires that
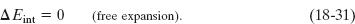
Figure 18-16 shows how such an expansion can be carried out. A gas, which is in thermal equilibrium within itself, is initially confined by a closed stopcock to one half of an insulated double chamber; the other half is evacuated. The stopcock is opened, and the gas expands freely to fill both halves of the chamber. No heat is transferred to or from the gas because of the insulation. No work is done by the gas because it rushes into a vacuum and thus does not meet any pressure.
A free expansion differs from all other processes we have considered because it cannot be done slowly and in a controlled way. As a result, at any given instant during the sudden expansion, the gas is not in thermal equilibrium and its pressure is not uniform. Thus, although we can plot the initial and final states on a p–V diagram, we cannot plot the expansion itself.
CHECKPOINT 6 For one complete cycle as shown in the p–V diagram here, are (a) ΔEint for the gas and (b) the net energy transferred as heat Q positive, negative, or zero?
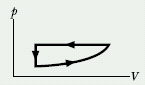
Let 1.00 kg of liquid water at 100°C be converted to steam at 100°C by boiling at standard atmospheric pressure (which is 1.00 atm or 1.01 × 105 Pa) in the arrangement of Fig. 18-17. The volume of that water changes from an initial value of 1.00 × 10−3 m3 as a liquid to 1.671 m3 as steam.
(a) How much work is done by the system during this process?
Solution: The Key Idea here is that the system must do positive work because the volume increases. In the general case we would calculate the work W done by integrating the pressure with respect to the volume (Eq. 18-25). However, here the pressure is constant at 1.01 × 105 Pa, so we can take p outside the integral. We then have
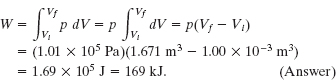
Fig. 18-17 Water boiling at constant pressure. Energy is transferred from the thermal reservoir as heat until the liquid water has changed completely into steam. Work is done by the expanding gas as it lifts the loaded piston.
(b) How much energy is transferred as heat during the process?
Solution: The Key Idea here is that the heat causes only a phase change and not a change in temperature, so it is given fully by Eq. 18-16 (Q = Lm). Because the change is from liquid to gaseous phase, L is the heat of vaporization LV, with the value given in Eq. 18-17 and Table 18-4. We find
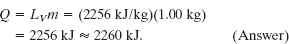
(c) What is the change in the system’s internal energy during the process?
Solution: The Key Idea here is that the change in the system’s internal energy is related to the heat (here, this is energy transferred into the system) and the work (here, this is energy transferred out of the system) by the first law of thermodynamics (Eq. 18-26). Thus, we can write

This quantity is positive, indicating that the internal energy of the system has increased during the boiling process. This energy goes into separating the H2O molecules, which strongly attract one another in the liquid state. We see that, when water is boiled, about 7.5% (= 169 kJ/2260 kJ) of the heat goes into the work of pushing back the atmosphere. The rest of the heat goes into the system’s internal energy.
Leave a Reply