If you have ever tried to sleep while someone played loud music nearby, you are well aware that there is more to sound than frequency, wavelength, and speed. There is also intensity. The intensity I of a sound wave at a surface is the average rate per unit area at which energy is transferred by the wave through or onto the surface. We can write this as
where P is the time rate of energy transfer (the power) of the sound wave and A is the area of the surface intercepting the sound. As we shall derive shortly, the intensity I is related to the displacement amplitude sm of the sound wave by
Variation of Intensity with Distance
How intensity varies with distance from a real sound source is often complex. Some real sources (like loudspeakers) may transmit sound only in particular directions, and the environment usually produces echoes (reflected sound waves) that overlap the direct sound waves. In some situations, however, we can ignore echoes and assume that the sound source is a point source that emits the sound isotropically—that is, with equal intensity in all directions. The wavefronts spreading from such an isotropic point source S at a particular instant are shown in Fig. 17-10.
Sound can cause the wall of a drinking glass to oscillate. If the sound produces a standing wave of oscillations and if the intensity of the sound is large enough, the glass will shatter.
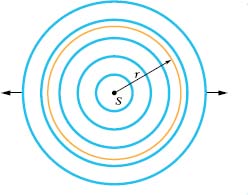
Fig. 17-10 A point source S emits sound waves uniformly in all directions. The waves pass through an imaginary sphere of radius r that is centered on S.
Let us assume that the mechanical energy of the sound waves is conserved as they spread from this source. Let us also center an imaginary sphere of radius r on the source, as shown in Fig. 17-10. All the energy emitted by the source must pass through the surface of the sphere. Thus, the time rate at which energy is transferred through the surface by the sound waves must equal the time rate at which energy is emitted by the source (that is, the power Ps of the source). From Eq. 17-26, the intensity I at the sphere must then be
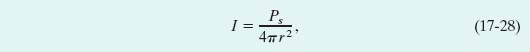
where 4πr2 is the area of the sphere. Equation 17-28 tells us that the intensity of sound from an isotropic point source decreases with the square of the distance r from the source.
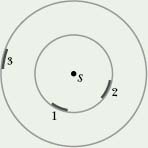
CHECKPOINT 3 The figure indicates three small patches 1, 2, and 3 that lie on the surfaces of two imaginary spheres; the spheres are centered on an isotropic point source S of sound. The rates at which energy is transmitted through the three patches by the sound waves are equal. Rank the patches according to (a) the intensity of the sound on them and (b) their area, greatest first.
The Decibel Scale
You saw in Sample Problem 17-2 that the displacement amplitude at the human ear ranges from about 10−5 m for the loudest tolerable sound to about 10−11 m for the faintest detectable sound, a ratio of 106. From Eq. 17-27 we see that the intensity of a sound varies as the square of its amplitude, so the ratio of intensities at these two limits of the human auditory system is 1012. Humans can hear over an enormous range of intensities.
We deal with such an enormous range of values by using logarithms. Consider the relation
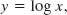
in which x and y are variables. It is a property of this equation that if we multiply x by 10, then y increases by 1. To see this, we write
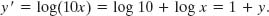
Similarly, if we multiply x by 1012, y increases by only 12.
Thus, instead of speaking of the intensity I of a sound wave, it is much more convenient to speak of its sound level β, defined as
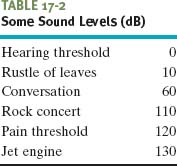
Here dB is the abbreviation for decibel, the unit of sound level, a name that was chosen to recognize the work of Alexander Graham Bell. I0 in Eq. 17-29 is a standard reference intensity (= 10−12 W/m2), chosen because it is near the lower limit of the human range of hearing. For I = I0, Eq. 17-29 gives β = 10 log 1 = 0, so our standard reference level corresponds to zero decibels. Then β increases by 10 dB every time the sound intensity increases by an order of magnitude (a factor of 10). Thus, β = 40 corresponds to an intensity that is 104 times the standard reference level. Table 17-2 lists the sound levels for a variety of environments.
Derivation of Eq. 17-27
Consider, in Fig. 17-5a, a thin slice of air of thickness dx, area A, and mass dm, oscillating back and forth as the sound wave of Eq. 17-13 passes through it. The kinetic energy dK of the slice of air is
Here νs is not the speed of the wave but the speed of the oscillating element of air, obtained from Eq. 17-13 as
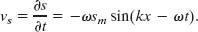
Using this relation and putting dm = ρA dx allow us to rewrite Eq. 17-30 as
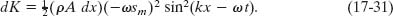
Dividing Eq. 17-31 by dt gives the rate at which kinetic energy moves along with the wave. As we saw in Lesson 16 for transverse waves, dx/dt is the wave speed ν, so we have
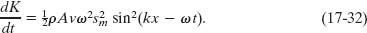
The average rate at which kinetic energy is transported is
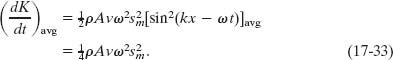
To obtain this equation, we have used the fact that the average value of the square of a sine (or a cosine) function over one full oscillation is 
.
We assume that potential energy is carried along with the wave at this same average rate. The wave intensity I, which is the average rate per unit area at which energy of both kinds is transmitted by the wave, is then, from Eq. 17-33,
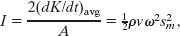
which is Eq. 17-27, the equation we set out to derive.
An electric spark jumps along a straight line of length L = 10 m, emitting a pulse of sound that travels radially outward from the spark. (The spark is said to be a line source of sound.) The power of the emission is Ps = 1.6 × 104 W.
(a) What is the intensity I of the sound when it reaches a distance r = 12 m from the spark?
Solution: Let us center an imaginary cylinder of radius r = 12 m and length L = 10 m (open at both ends) on the spark, as shown in Fig. 17-11. One Key Idea here is that the intensity I at the cylindrical surface is the ratio P/A, where P is the time rate at which sound energy passes through the surface and A is the surface area. Another Key Idea is to assume that the principle of conservation of energy applies to the sound energy. This means that the rate P at which energy is transferred through the cylinder must equal the rate Ps at which energy is emitted by the source. Putting these ideas together and noting that the area of the cylindrical surface is A = 2πrL, we have
This tells us that the intensity of the sound from a line source decreases with distance r (and not with the square of distance r as for a point source). Substituting the given data, we find
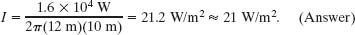
(b) At what time rate Pd is sound energy intercepted by an acoustic detector of area Ad = 2.0 cm2, aimed at the spark and located a distance r = 12 m from the spark?
Solution: Applying the first Key Idea of part (a), we know that the intensity of sound at the detector is the ratio of the energy transfer rate Pd there to the detector’s area Ad:
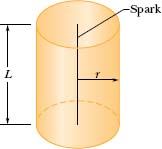
Fig. 17-11 A spark along a straight line of length L emits sound waves radially outward. The waves pass through an imaginary cylinder of radius r and length L that is centered on the spark.
We can imagine that the detector lies on the cylindrical surface of (a). Then the sound intensity at the detector is the intensity I (= 21.2 W/m2) at the cylindrical surface. Solving Eq. 17-35 for Pd gives us
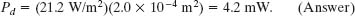
Many veteran rockers suffer from acute hearing damage because of the high sound levels they endured for years while playing music near loudspeakers or listening to music on headphones. Some, like Ted Nugent, can no longer hear in a damaged ear. Others, like Peter Townshend of the Who, have a continuous ringing sensation (tinnitus). Recently, many rockers, such as Lars Ulrich of Metallica (Fig. 17-12), began wearing special earplugs to protect their hearing during performances. If an earplug decreases the sound level of the sound waves by 20 dB, what is the ratio of the final intensity If of the waves to their initial intensity Ii?
Solution: The Key Idea here is that for both the final and initial waves, the sound level β is related to the intensity by the definition of sound level in Eq. 17-29. For the final waves we have
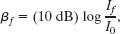
and for the initial waves we have
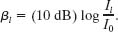
The difference in the sound levels is
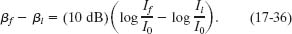
Using the identity
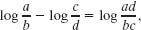
we can rewrite Eq. 17-36 as
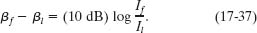
Rearranging and then substituting the given decrease in sound level as βf − βi = −20 dB, we find
Fig. 17-12 Lars Ulrich of Metallica is an advocate for the organization HEAR (Hearing Education and Awareness for Rockers), which warns about the damage high sound levels can have on hearing.
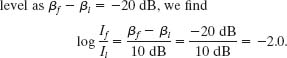
We next take the antilog of the far left and far right sides of this equation. (Although the antilog 10−2.0 can be evaluated mentally, you could use a calculator by keying in 10^-2.0 or using the 10x key.) We find
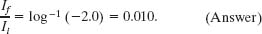
Thus, the earplug reduces the intensity of the sound waves to 0.010 of their initial intensity, which is a decrease of two orders of magnitude.
Leave a Reply