Like transverse waves, sound waves can undergo interference. Let us consider, in particular, the interference between two identical sound waves traveling in the same direction. Figure 17-8 shows how we can set up such a situation: Two point sources S1 and S2 emit sound waves that are in phase and of identical wavelength λ. Thus, the sources themselves are said to be in phase; that is, as the waves emerge from the sources, their displacements are always identical. We are interested in the waves that then travel through point P in Fig. 17-8. We assume that the distance to P is much greater than the distance between the sources so that we can approximate the waves as traveling in the same direction at P.
If the waves traveled along paths with identical lengths to reach point P, they would be in phase there. As with transverse waves, this means that they would undergo fully constructive interference there. However, in Fig. 17-8, path L2 traveled by the wave from S2 is longer than path L1 traveled by the wave from S1. The difference in path lengths means that the waves may not be in phase at point P. In other words, their phase difference ![]() at P depends on their path length difference ΔL = |L2 − L1|.
at P depends on their path length difference ΔL = |L2 − L1|.
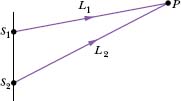
Fig. 17-8 Two point sources S1 and S2 emit spherical sound waves in phase. The rays indicate that the waves pass through a common point P.
To relate phase difference ![]() to path length difference ΔL, we recall (from Section 16-4) that a phase difference of 2π rad corresponds to one wavelength. Thus, we can write the proportion
to path length difference ΔL, we recall (from Section 16-4) that a phase difference of 2π rad corresponds to one wavelength. Thus, we can write the proportion

from which
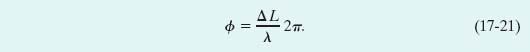
Fully constructive interference occurs when ![]() is zero, 2π, or any integer multiple of 2π. We can write this condition as
is zero, 2π, or any integer multiple of 2π. We can write this condition as

From Eq. 17-21, this occurs when the ratio ΔL/λ is

For example, if the path length difference ΔL = |L2 − L1| in Fig. 17-8 is equal to 2λ, then ΔL/λ = 2 and the waves undergo fully constructive interference at point P. The interference is fully constructive because the wave from S2 is phase shifted relative to the wave from S1 by 2λ, putting the two waves exactly in phase at P.
Fully destructive interference occurs when ![]() is an odd multiple of π, a condition we can write as
is an odd multiple of π, a condition we can write as

From Eq. 17-21, this occurs when the ratio ΔL/λ is

For example, if the path length difference ΔL = |L2 − L1| in Fig. 17-8 is equal to 2.5λ, then ΔL/λ = 2.5 and the waves undergo fully destructive interference at point P. The interference is fully destructive because the wave from S2 is phase-shifted relative to the wave from S1 by 2.5 wavelengths, which puts the two waves exactly out of phase at P.
Of course, two waves could produce intermediate interference as, say, when ΔL/λ = 1.2. This would be closer to fully constructive interference (ΔL/λ = 1.0) than to fully destructive interference (ΔL/λ = 1.5).
In Fig. 17-9a, two point sources S1 and S2, which are in phase and separated by distance D = 1.5λ, emit identical sound waves of wavelength λ.
(a) What is the path length difference of the waves from S1 and S2 at point P1, which lies on the perpendicular bisector of distance D, at a distance greater than D from the sources? What type of interference occurs at P1?
Solution: The Key Idea here is that, because the waves travel identical distances to reach P1, their path length difference is

From Eq. 17-23, this means that the waves undergo fully constructive interference at P1.
(b) What are the path length difference and type of interference at point P2 in Fig. 17-9a?
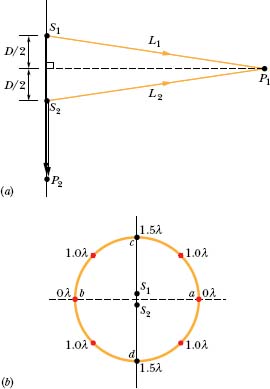
Fig. 17-9 (a) Two point sources S1 and S2, separated by distance D, emit spherical sound waves in phase. The waves travel equal distances to reach point P1. Point P2 is on the line extending through S1 and S2. (b) The path length difference (in terms of wavelength) between the waves from S1 and S2, at eight points on a large circle around the sources.
Solution: Now the Key Idea is that the wave from S1 travels the extra distance D (= 1.5λ) to reach P2. Thus, the path length difference is

From Eq. 17-25, this means that the waves are exactly out of phase at P2 and undergo fully destructive interference there.
(c) Figure 17-9b shows a circle with a radius much greater than D, centered on the midpoint between sources S1 and S2. What is the number of points N around this circle at which the interference is fully constructive?
Solution: Imagine that, starting at point a, we move clockwise along the circle to point d. One Key Idea here is that as we move to point d, the path length difference ΔL increases and so the type of interference changes. From (a), we know that the path length difference is ΔL = 0λ at point a. From (b), we know that ΔL = 1.5λ at point d. Thus, there must be one point along the circle between a and d at which ΔL = λ, as indicated in Fig. 17-9b. From Eq. 17-23, fully constructive interference occurs at that point. Also, there can be no other point along the way from point a to point d at which fully constructive interference occurs, because there is no other integer than 1 between 0 and 1.5.
Another Key Idea here is to use symmetry to locate the other points of fully constructive interference along the rest of the circle. Symmetry about line cd gives us point b, at which ΔL = 0λ. Also, there are three more points at which ΔL = λ. In all we have

![]() CHECKPOINT 2 In this sample problem, if the distance D between sources S1 and S2 were, instead, equal to 4λ, what would be the path length difference and what type of interference would occur at (a) point P1 and (b) point P2
CHECKPOINT 2 In this sample problem, if the distance D between sources S1 and S2 were, instead, equal to 4λ, what would be the path length difference and what type of interference would occur at (a) point P1 and (b) point P2
Leave a Reply