The Wave Equation

As a wave passes through any element on a stretched string, the element moves perpendicularly to the wave’s direction of travel. By applying Newton’s second law to the element’s motion, we can derive a general differential equation, called the wave equation, that governs the travel of waves of any type.

Figure 16-13a shows a snapshot of a string element of mass dm and length ℓ as a wave travels along a string of linear density μ that is stretched along a horizontal x axis. Let us assume that the wave amplitude is small so that the element can be tilted only slightly from the x axis as the wave passes. The force  on the right end of the element has a magnitude equal to tension τ in the string and is directed slightly upward. The force  on the left end of the element also has a magnitude equal to the tension τ but is directed slightly downward. Because of the slight curvature of the element, these two forces produce a net force that causes the element to have an upward acceleration a_y. Newton’s second law written for y components (F_net,y = ma_y) gives us

Let’s analyze this equation in parts.

Mass. The element’s mass dm can be written in terms of the string’s linear density μ and the element’s length ℓ as dm = μℓ. Because the element can have only a slight tilt, ℓ ≈ dx (Fig. 16-13a) and we have the approximation

Acceleration. The acceleration a_y in Eq. 16-34 is the second derivative of the displacement y with respect to time:

Forces. Figure 16-13b shows that  is tangent to the string at the right end of the string element. Thus we can relate the components of the force to the string slope S₂ at the right end as

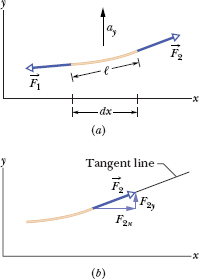
Fig. 16-13 (a) A string element as a sinusoidal transverse wave travels on a stretched string. Forces  and  act at the left and right ends, producing acceleration  having a vertical component a_y. (b) The force at the element’s right end is directed along a tangent to the element’s right side.

We can also relate the components to the magnitude F₂ (= τ) with

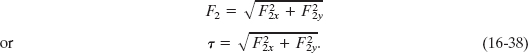
However, because we assume that the element is only slightly tilted, F_2y  F_2x and therefore we can rewrite Eq. 16-38 as

Substituting this into Eq. 16-37 and solving for F_2y yield

Similar analysis at the left end of the string element gives us

We can now substitute Eqs. 16-35, 16-36, 16-40, and 16-41 into Eq. 16-34 to write

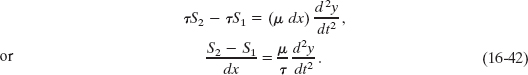
Because the string element is short, slopes S₂ and S₁ differ by only a differential amount dS, where S is the slope at any point:

First replacing S₂ − S₁ in Eq. 16-42 with dS and then using Eq. 16-43 to substitute dy/dx for S, we find

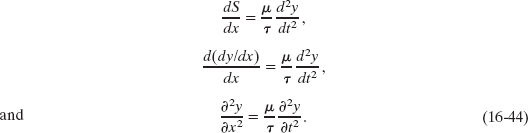
In the last step, we switched to the notation of partial derivatives because on the left we differentiate only with respect to x and on the right we differentiate only with respect to t. Finally, substituting from Eq. 16-26 , we find

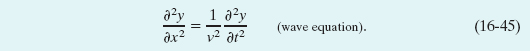
This is the general differential equation that governs the travel of waves of all types.