Figure 16-8 shows two snapshots of the wave of Eq. 16-2, taken a small time interval Δt apart. The wave is traveling in the positive direction of x (to the right in Fig. 16-8), the entire wave pattern moving a distance Δx in that direction during the interval Δt. The ratio Δx/Δt (or, in the differential limit, dx/dt) is the wave speed v. How can we find its value?
As the wave in Fig. 16-8 moves, each point of the moving wave form, such as point A marked on a peak, retains its displacement y. (Points on the string do not retain their displacement, but points on the wave form do.) If point A retains its displacement as it moves, the phase in Eq. 16-2 giving it that displacement must remain a constant:
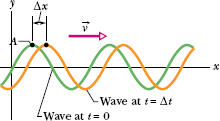
Fig. 16-8 Two snapshots of the wave of Fig. 16-5, at time t = 0 and then at time t = Δt. As the wave moves to the right at velocity  , the entire curve shifts a distance Δx during Δt. Point A “rides” with the wave form, but the string elements move only up and down.
, the entire curve shifts a distance Δx during Δt. Point A “rides” with the wave form, but the string elements move only up and down.

Note that although this argument is constant, both x and t are changing. In fact, as t increases, x must also, to keep the argument constant. This confirms that the wave pattern is moving in the positive direction of x.
To find the wave speed v, we take the derivative of Eq. 16-11, getting
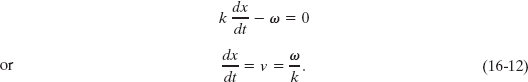
Using Eq. 16-5 (k = 2π/λ) and Eq. 16-8 (ω = 2π/T), we can rewrite the wave speed as
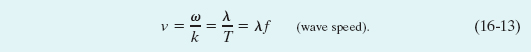
The equation v = λ/T tells us that the wave speed is one wavelength per period; the wave moves a distance of one wavelength in one period of oscillation.
Equation 16-2 describes a wave moving in the positive direction of x. We can find the equation of a wave traveling in the opposite direction by replacing t in Eq. 16-2 with −t. This corresponds to the condition

which (compare Eq. 16-11) requires that x decrease with time. Thus, a wave traveling in the negative direction of x is described by the equation
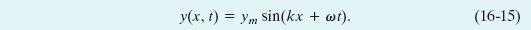
If you analyze the wave of Eq. 16-15 as we have just done for the wave of Eq. 16-2, you will find for its velocity

The minus sign (compare Eq. 16-12) verifies that the wave is indeed moving in the negative direction of x and justifies our switching the sign of the time variable.
Consider now a wave of arbitrary shape, given by

where h represents any function, the sine function being one possibility. Our previous analysis shows that all waves in which the variables x and t enter into the combination kx ± ωt are traveling waves. Furthermore, all traveling waves must be of the form of Eq. 16-17. Thus, ![]() represents a possible (though perhaps physically a little bizarre) traveling wave. The function y(x, t) = sin(ax2 − bt), on the other hand, does not represent a traveling wave.
represents a possible (though perhaps physically a little bizarre) traveling wave. The function y(x, t) = sin(ax2 − bt), on the other hand, does not represent a traveling wave.
A wave traveling along a string is described by
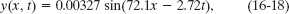
in which the numerical constants are in SI units (0.00327 m, 72.1 rad/m, and 2.72 rad/s).
(a) What is the amplitude of this wave?
Solution: The Key Idea is that Eq. 16-18 is of the same form as Eq. 16-2,
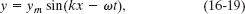
so we have a sinusoidal wave. By comparing the two equations, we see that the amplitude is
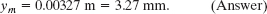
(b) What are the wavelength, period, and frequency of this wave?
Solution: By comparing Eqs. 16-18 and 16-19, we see that the angular wave number and angular frequency are
k = 72.1 rad/m and ω = 2.72 rad/s.
We then relate wavelength λ to k via Eq. 16-5:

Next, we relate T to ω with Eq. 16-8:
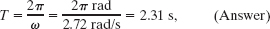
and from Eq. 16-9 we have
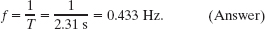
(c) What is the velocity of this wave?
Solution: The speed of the wave is given by Eq. 16-13:
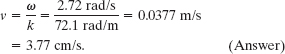
Because the phase in Eq. 16-18 contains the position variable x, the wave is moving along the x axis. Also, because the wave equation is written in the form of Eq. 16-2, the minus sign in front of the ωt term indicates that the wave is moving in the positive direction of the x axis. (Note that the quantities calculated in (b) and (c) are independent of the amplitude of the wave.)
(d) What is the displacement y at x = 22.5 cm and t = 18.9 s?
Solution: The Key Idea here is that Eq. 16-18 gives the displacement as a function of position x and time t. Substituting the given values into the equation yields
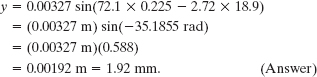
Thus, the displacement is positive. (Be sure to change your calculator mode to radians before evaluating the sine.)
In Sample Problem 16-2d, we showed that at t = 18.9 s the transverse displacement y of the element of the string at x = 0.255 m due to the wave of Eq. 16-18 is 1.92 mm.
(a) What is u, the transverse velocity of the same element of the string, at that time? (This velocity, which is associated with the transverse oscillation of an element of the string, is in the y direction. Do not confuse it with v, the constant velocity at which the wave form travels along the x axis.)
Solution: The Key Idea here is that the transverse velocity u is the rate at which the displacement y of the element is changing. In general, that displacement is given by
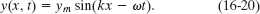
For an element at a certain location x, we find the rate of change of y by taking the derivative of Eq. 16-20 with respect to t while treating x as a constant. A derivative taken while one (or more) of the variables is treated as a constant is called a partial derivative and is represented by the symbol ∂/∂x rather than d/dx. Here we have
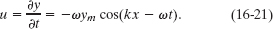
Next, substituting numerical values from Sample Problem 16-2, we obtain
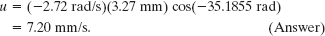
Thus, at t = 18.9 s, the element of the string at x = 22.5 cm is moving in the positive direction of y with a speed of 7.20 mm/s.
(b) What is the transverse acceleration ay of the same element at that time?
Solution: The Key Idea here is that the transverse acceleration ay is the rate at which the transverse velocity of the element is changing. From Eq. 16-21, again treating x as a constant but allowing t to vary, we find
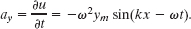
Comparison with Eq. 16-20 shows that we can write this as

We see that the transverse acceleration of an oscillating string element is proportional to its transverse displacement but opposite in sign. This is completely consistent with the action of the element itself—namely, that it is moving transversely in simple harmonic motion. Substituting numerical values yields
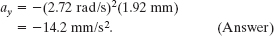
Thus, at t = 18.9 s, the element of string at x = 22.5 cm is displaced from its equilibrium position by 1.92 mm in the positive y direction and has an acceleration of magnitude 14.2 mm/s2 in the negative y direction.
![]() CHECK POINT 2 Here are the equations of three waves:
CHECK POINT 2 Here are the equations of three waves:
(1) y(x, t) = 2 sin(4x − 2t),
(2) y(x, t) = sin(3x − 4t),
(3) y(x, t) = 2 sin(3x − 3t).
Rank the waves according to their (a) wave speed and (b) maximum transverse speed, greatest first.
PROBLEM-SOLVING TACTICS
TACTIC 1: Evaluating Large Phases
Sometimes, as in Sample Problems 16-2d and 16-3, an angle much greater than 2π rad (or 360º) crops up and you are asked to find its sine or cosine. Adding or subtracting an integral multiple of 2π rad to such an angle does not change the value of any of its trigonometric functions. In Sample Problem 16-2d, for example, we used the angle −35.1855 rad in a sine function. Adding (6)(2π rad) to this angle yields
−35.1855 rad + (6)(2π rad) = 2.51361 rad,
an angle of less than 2π rad that has the same trigonometric functions as −35.1855 rad (Fig. 16-9). As an example, the sine of both 2.51361 rad and −35.1855 rad is 0.588.
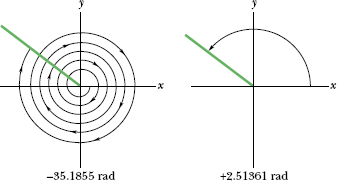
Fig. 16-9 These two angles are different, but all their trigonometric functions are identical.
Your calculator will reduce such large angles for you automatically. Caution: Do not round off large angles if you intend to take their sines or cosines. In taking the sine of a very large angle, you are throwing away most of the angle and taking the sine of what is left over. If, for example, you were to round −35.1855 rad to −35 rad (a change of 0.5% and normally a reasonable step), you would be changing the sine of the angle by 27%. Also, if you change a large angle from degrees to radians, be sure to use an exact conversion factor (such as 180º = π rad) rather than an approximate one (such as 57.3º ≈ 1 rad).
Leave a Reply