A pendulum will swing only briefly underwater, because the water exerts on the pendulum a drag force that quickly eliminates the motion. A pendulum swinging in air does better, but still the motion dies out eventually, because the air exerts a drag force on the pendulum (and friction acts at its support point), transferring energy from the pendulum’s motion.
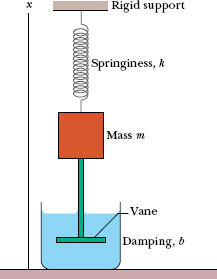
Fig. 15-15 An idealized damped simple harmonic oscillator. A vane immersed in a liquid exerts a damping force on the block as the block oscillates parallel to the x axis.
When the motion of an oscillator is reduced by an external force, the oscillator and its motion are said to be damped. An idealized example of a damped oscillator is shown in Fig. 15-15, where a block with mass m oscillates vertically on a spring with spring constant k. From the block, a rod extends to a vane (both assumed massless) that is submerged in a liquid. As the vane moves up and down, the liquid exerts an inhibiting drag force on it and thus on the entire oscillating system. With time, the mechanical energy of the block–spring system decreases, as energy is transferred to thermal energy of the liquid and vane.
Let us assume the liquid exerts a damping force ![]() that is proportional to the velocity
that is proportional to the velocity ![]() of the vane and block (an assumption that is accurate if the vane moves slowly). Then, for components along the x axis in Fig. 15-15, we have
of the vane and block (an assumption that is accurate if the vane moves slowly). Then, for components along the x axis in Fig. 15-15, we have

where b is a damping constant that depends on the characteristics of both the vane and the liquid and has the SI unit of kilogram per second. The minus sign indicates that ![]() opposes the motion.
opposes the motion.
The force on the block from the spring is Fs = −kx. Let us assume that the gravitational force on the block is negligible relative to Fd and Fs. Then we can write Newton’s second law for components along the x axis (Fnet,x = max) as

Substituting dx/dt for v and d2x/dt2 for a and rearranging give us the differential equation
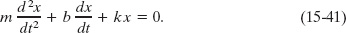
The solution of this equation is

where xm is the amplitude and ω′ is the angular frequency of the damped oscillator. This angular frequency is given by
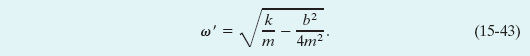
If b = 0 (there is no damping), then Eq. 15-43 reduces to Eq. 15-12 ![]() for the angular frequency of an undamped oscillator, and Eq. 15-42 reduces to Eq. 15-3 for the displacement of an undamped oscillator. If the damping constant is small but not zero (so that
for the angular frequency of an undamped oscillator, and Eq. 15-42 reduces to Eq. 15-3 for the displacement of an undamped oscillator. If the damping constant is small but not zero (so that ![]() ), then ω′ ≈ ω.
), then ω′ ≈ ω.
We can regard Eq. 15-42 as a cosine function whose amplitude, which is xm e−bt/2m, gradually decreases with time, as Fig. 15-16 suggests. For an undamped oscillator, the mechanical energy is constant and is given by Eq. 15-21 ![]() . If the oscillator is damped, the mechanical energy is not constant but decreases with time. If the damping is small, we can find E(t) by replacing xm in Eq. 15-21 with xm e−bt/2m, the amplitude of the damped oscillations. By doing so, we find that
. If the oscillator is damped, the mechanical energy is not constant but decreases with time. If the damping is small, we can find E(t) by replacing xm in Eq. 15-21 with xm e−bt/2m, the amplitude of the damped oscillations. By doing so, we find that
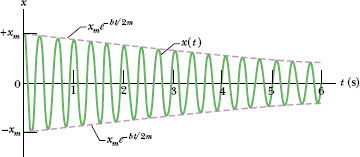
Fig. 15-16 The displacement function x(t) for the damped oscillator of Fig. 15-15, with values given in Sample Problem 15-7. The amplitude, which is xm e−bt/2m, decreases exponentially with time.
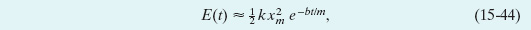
which tells us that, like the amplitude, the mechanical energy decreases exponentially with time.
![]() CHECKPOINT 5 Here are three sets of values for the spring constant, damping constant, and mass for the damped oscillator of Fig. 15-15. Rank the sets according to the time required for the mechanical energy to decrease to one-fourth of its initial value, greatest first.
CHECKPOINT 5 Here are three sets of values for the spring constant, damping constant, and mass for the damped oscillator of Fig. 15-15. Rank the sets according to the time required for the mechanical energy to decrease to one-fourth of its initial value, greatest first.

For the damped oscillator of Fig. 15-15, m = 250 g, k = 85 N/m, and b = 70 g/s.
(a) What is the period of the motion?
Solution: The Key Idea here is that because ![]() kg/s, the period is approximately that of the undamped oscillator. From Eq. 15-13, we then have
kg/s, the period is approximately that of the undamped oscillator. From Eq. 15-13, we then have

(b) How long does it take for the amplitude of the damped oscillations to drop to half its initial value?
Solution: Now the Key Idea is that the amplitude at time t is displayed in Eq. 15-42 as xm e−bt/2m. It has the value xm at t = 0. Thus, we must find the value of t for which
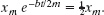
Canceling xm and taking the natural logarithm of the equation that remains, we have ln ![]() on the right side and
on the right side and
ln(e−bt/2m) = −bt/2m
on the left side. Thus,

Because T = 0.34 s, this is about 15 periods of oscillation.
(c) How long does it take for the mechanical energy to drop to one-half its initial value?
Solution: Here the Key Idea is that, from Eq. 15-44, the mechanical energy at time t is ![]() . It has the value
. It has the value ![]() at t = 0. Thus, we must find the value of t for which
at t = 0. Thus, we must find the value of t for which
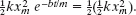
If we divide both sides of this equation by ![]() and solve for t as we did above, we find
and solve for t as we did above, we find
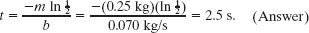
This is exactly half the time we calculated in (b), or about 7.5 periods of oscillation. Figure 15-16 was drawn to illustrate this sample problem.
Leave a Reply