Figure 14-9 shows a student in a swimming pool, manipulating a very thin plastic sack (of negligible mass) that is filled with water. She finds that the sack and its contained water are in static equilibrium, tending neither to rise nor to sink. The downward gravitational force ![]() on the contained water must be balanced by a net upward force from the water surrounding the sack.
on the contained water must be balanced by a net upward force from the water surrounding the sack.
This net upward force is a buoyant force ![]() . It exists because the pressure in the surrounding water increases with depth below the surface. Thus, the pressure near the bottom of the sack is greater than the pressure near the top, which means the forces on the sack due to this pressure are greater in magnitude near the bottom of the sack than near the top. Some of the forces are represented in Fig. 14-10a, where the space occupied by the sack has been left empty. Note that the force vectors drawn near the bottom of that space (with upward components) have longer lengths than those drawn near the top of the sack (with downward components). If we vectorially add all the forces on the sack from the water, the horizontal components cancel and the vertical components add to yield the upward buoyant force
. It exists because the pressure in the surrounding water increases with depth below the surface. Thus, the pressure near the bottom of the sack is greater than the pressure near the top, which means the forces on the sack due to this pressure are greater in magnitude near the bottom of the sack than near the top. Some of the forces are represented in Fig. 14-10a, where the space occupied by the sack has been left empty. Note that the force vectors drawn near the bottom of that space (with upward components) have longer lengths than those drawn near the top of the sack (with downward components). If we vectorially add all the forces on the sack from the water, the horizontal components cancel and the vertical components add to yield the upward buoyant force ![]() on the sack. (Force
on the sack. (Force ![]() is shown to the right of the pool in Fig. 14-10a.)
is shown to the right of the pool in Fig. 14-10a.)
Because the sack of water is in static equilibrium, the magnitude of ![]() is equal to the magnitude mfg of the gravitational force
is equal to the magnitude mfg of the gravitational force ![]() on the sack of water: Fb = mfg. (Subscript f refers to fluid, here the water.) In words, the magnitude of the buoyant force is equal to the weight of the water in the sack.
on the sack of water: Fb = mfg. (Subscript f refers to fluid, here the water.) In words, the magnitude of the buoyant force is equal to the weight of the water in the sack.
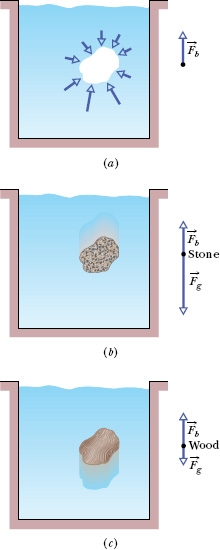
Fig. 14-10 (a) The water surrounding the hole in the water produces a net upward buoyant force on whatever fills the hole. (b) For a stone of the same volume as the hole, the gravitational force exceeds the buoyant force in magnitude. (c) For a lump of wood of the same volume, the gravitational force is less than the buoyant force in magnitude.
In Fig. 14-10b, we have replaced the sack of water with a stone that exactly fills the hole in Fig. 14-10a. The stone is said to displace the water, meaning that the stone occupies space that would otherwise be occupied by water. We have changed nothing about the shape of the hole, so the forces at the hole’s surface must be the same as when the water-filled sack was in place. Thus, the same upward buoyant force that acted on the water-filled sack now acts on the stone; that is, the magnitude Fb of the buoyant force is equal to mfg, the weight of the water displaced by the stone.
Unlike the water-filled sack, the stone is not in static equilibrium. The downward gravitational force ![]() on the stone is greater in magnitude than the upward buoyant force, as is shown in the free-body diagram in Fig. 14-10b. The stone thus accelerates downward, sinking to the bottom of the pool.
on the stone is greater in magnitude than the upward buoyant force, as is shown in the free-body diagram in Fig. 14-10b. The stone thus accelerates downward, sinking to the bottom of the pool.
Let us next exactly fill the hole in Fig. 14-10a with a block of lightweight wood, as in Fig. 14-10c. Again, nothing has changed about the forces at the hole’s surface, so the magnitude Fb of the buoyant force is still equal to mfg, the weight of the displaced water. Like the stone, the block is not in static equilibrium. However, this time the gravitational force ![]() is lesser in magnitude than the buoyant force (as shown to the right of the pool), and so the block accelerates upward, rising to the top surface of the water.
is lesser in magnitude than the buoyant force (as shown to the right of the pool), and so the block accelerates upward, rising to the top surface of the water.
Our results with the sack, stone, and block apply to all fluids and are summarized in Archimedes’ principle:
![]() When a body is fully or partially submerged in a fluid, a buoyant force
When a body is fully or partially submerged in a fluid, a buoyant force ![]() from the surrounding fluid acts on the body. The force is directed upward and has a magnitude equal to the weight mfg of the fluid that has been displaced by the body.
from the surrounding fluid acts on the body. The force is directed upward and has a magnitude equal to the weight mfg of the fluid that has been displaced by the body.
The buoyant force on a body in a fluid has the magnitude
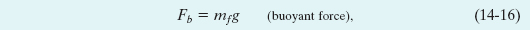
where mf is the mass of the fluid that is displaced by the body.
Floating
When we release a block of lightweight wood just above the water in a pool, the block moves into the water because the gravitational force on it pulls it downward. As the block displaces more and more water, the magnitude Fb of the upward buoyant force acting on it increases. Eventually, Fb is large enough to equal the magnitude Fg of the downward gravitational force on the block, and the block comes to rest. The block is then in static equilibrium and is said to be floating in the water. In general,
![]() When a body floats in a fluid, the magnitude Fb of the buoyant force on the body is equal to the magnitude Fg of the gravitational force on the body.
When a body floats in a fluid, the magnitude Fb of the buoyant force on the body is equal to the magnitude Fg of the gravitational force on the body.
We can write this statement as

From Eq. 14-16, we know that Fb = mfg. Thus,
![]() When a body floats in a fluid, the magnitude Fg of the gravitational force on the body is equal to the weight mfg of the fluid that has been displaced by the body.
When a body floats in a fluid, the magnitude Fg of the gravitational force on the body is equal to the weight mfg of the fluid that has been displaced by the body.
We can write this statement as

In other words, a floating body displaces its own weight of fluid.
Apparent Weight in a Fluid
If we place a stone on a scale that is calibrated to measure weight, then the reading on the scale is the stone’s weight. However, if we do this underwater, the upward buoyant force on the stone from the water decreases the reading. That reading is then an apparent weight. In general, an apparent weight is related to the actual weight of a body and the buoyant force on the body by
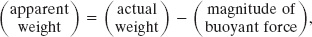
which we can write as
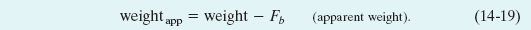
If, in some test of strength, you had to lift a heavy stone, you could do it more easily with the stone underwater. Then your applied force would need to exceed only the stone’s apparent weight, not its larger actual weight, because the upward buoyant force would help you lift the stone.
The magnitude of the buoyant force on a floating body is equal to the body’s weight. Equation 14-19 thus tells us that a floating body has an apparent weight of zero—the body would produce a reading of zero on a scale. (When astronauts prepare to perform a complex task in space, they practice the task floating underwater, where their apparent weight is zero as it is in space.)
![]() CHECKPOINT 2 A penguin floats first in a fluid of density ρ0, then in a fluid of density 0.95ρ0, and then in a fluid of density 1.1ρ0. (a) Rank the densities according to the magnitude of the buoyant force on the penguin, greatest first. (b) Rank the densities according to the amount of fluid displaced by the penguin, greatest first.
CHECKPOINT 2 A penguin floats first in a fluid of density ρ0, then in a fluid of density 0.95ρ0, and then in a fluid of density 1.1ρ0. (a) Rank the densities according to the magnitude of the buoyant force on the penguin, greatest first. (b) Rank the densities according to the amount of fluid displaced by the penguin, greatest first.
What fraction of the volume of an iceberg floating in seawater is visible?
Solution: Let Vi be the total volume of the iceberg. The nonvisible portion is below water, and thus the volume of this portion is equal to the volume Vf of the fluid (the seawater) displaced by the iceberg. We seek the fraction (call it frac)
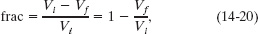
but we know neither volume. A Key Idea here is that, because the iceberg is floating, Eq. 14-18 (Fg = mfg) applies. We can write that equation as
mig = mfg,
from which we see that mi = mf. Thus, the mass of the iceberg is equal to the mass of the displaced fluid (seawater). Although we know neither mass, we can relate them to the densities of ice and seawater given in Table 14-1 by using Eq. 14-2 (ρ = m/V). Because mi = mf, we can write
ρiVi = ρfVf
or
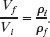
Substituting this into Eq. 14-20 and then using the known densities, we find
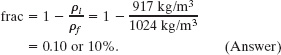
A spherical, helium-filled balloon has a radius R of 12.0 m. The balloon, support cables, and basket have a mass m of 196 kg. What maximum load M can the balloon support while it floats at an altitude at which the helium density ρHe is 0.160 kg/m3 and the air density ρair is 1.25 kg/m3? Assume that only the balloon displaces air.
Solution: The Key Idea here is that the balloon, cables, basket, load, and the contained helium form a floating body, with a total mass of m + M + mHe, where mHe is the mass of the contained helium. Then the magnitude of the total gravitational force on this body must be equal to the weight of the air displaced by the body (the air is the fluid in which this body floats). Let mair be the mass of the air displaced by the body. From Eq. 14-18 (Fg = mfg), we have
(m + M + mHe)g = mairg
or
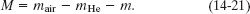
We do not know mHe and mair but we do know the corresponding densities; so we can use Eq. 14-2 (ρ = m/V) to rewrite Eq. 14-21 in terms of those densities. First we note that, because the load, support cables, and basket displace a negligible amount of air, the volume of the displaced air is equal to the volume ![]() of the spherical balloon. Then Eq. 14-21 becomes
of the spherical balloon. Then Eq. 14-21 becomes
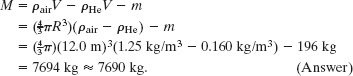

Fig. 14-11 At a certain point, the rising flow of smoke and heated gas changes from steady to turbulent.
Leave a Reply