Measuring Pressure

The Mercury Barometer

Figure 14-5a shows a very basic mercury barometer, a device used to measure the pressure of the atmosphere. The long glass tube is filled with mercury and inverted with its open end in a dish of mercury, as the figure shows. The space above the mercury column contains only mercury vapor, whose pressure is so small at ordinary temperatures that it can be neglected.

We can use Eq. 14-7 to find the atmospheric pressure p₀ in terms of the height h of the mercury column. We choose level 1 of Fig. 14-2 to be that of the air–mercury interface and level 2 to be that of the top of the mercury column, as labeled in Fig. 14-5a. We then substitute

y₁ = 0,  p₁ = p₀  and  y₂ = h,  p₂ = 0

into Eq. 14-7, finding that

where ρ is the density of the mercury.

For a given pressure, the height h of the mercury column does not depend on the cross-sectional area of the vertical tube. The fanciful mercury barometer of Fig. 14-5b gives the same reading as that of Fig. 14-5a; all that counts is the vertical distance h between the mercury levels.

Equation 14-9 shows that, for a given pressure, the height of the column of mercury depends on the value of g at the location of the barometer and on the density of mercury, which varies with temperature. The height of the column (in millimeters) is numerically equal to the pressure (in torr) only if the barometer is at a place where g has its accepted standard value of 9.80665 m/s² and the temperature of the mercury is 0°C. If these conditions do not prevail (and they rarely do), small corrections must be made before the height of the mercury column can be transformed into a pressure.

The Open-Tube Manometer

An open-tube manometer (Fig. 14-6) measures the gauge pressure p_g of a gas. It consists of a ∪-tube containing a liquid, with one end of the tube connected to the vessel whose gauge pressure we wish to measure and the other end open to the atmosphere. We can use Eq. 14-7 to find the gauge pressure in terms of the height h shown in Fig. 14-6. Let us choose levels 1 and 2 as shown in Fig. 14-6. We then substitute

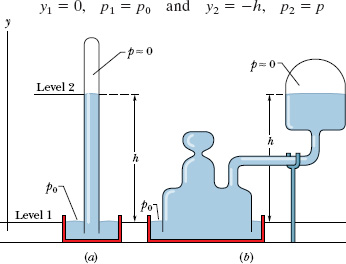
Fig. 14-5 (a) A mercury barometer. (b) Another mercury barometer. The distance h is the same in both cases.

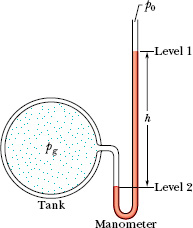
Fig. 14-6 An open-tube manometer, connected to measure the gauge pressure of the gas in the tank on the left. The right arm of the ∪-tube is open to the atmosphere.

into Eq. 14-7, finding that

where ρ is the density of the liquid in the tube. The gauge pressure p_g is directly proportional to h.

The gauge pressure can be positive or negative, depending on whether p > p₀ or p < p₀. In inflated tires or the human circulatory system, the (absolute) pressure is greater than atmospheric pressure, so the gauge pressure is a positive quantity, sometimes called the overpressure. If you suck on a straw to pull fluid up the straw, the (absolute) pressure in your lungs is actually less than atmospheric pressure. The gauge pressure in your lungs is then a negative quantity.

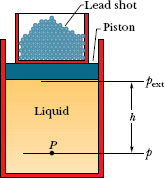
Fig. 14-7 Lead shot (small balls of lead) loaded onto the piston create a pressure p_ext at the top of the en closed (incompressible) liquid. If p_ext is increased, by adding more lead shot, the pressure increases by the same amount at all points within the liquid.