Gravitation Near Earth’s Surface

Let us assume that Earth is a uniform sphere of mass M. The magnitude of the gravitational force from Earth on a particle of mass m, located outside Earth a distance r from Earth’s center, is then given by Eq. 13-1 as

If the particle is released, it will fall toward the center of Earth, as a result of the gravitational force , with an acceleration we shall call the gravitational acceleration . Newton’s second law tells us that magnitudes F and a_g are related by

Now, substituting F from Eq. 13-9 into Eq. 13-10 and solving for a_g, we find

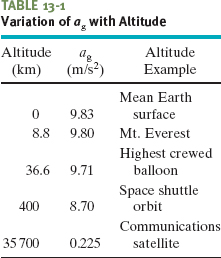
Table 13-1 shows values of a_g computed for various altitudes above Earth’s surface. Notice a_g is significant even at 400 km.

Since Section 5-4, we have assumed that Earth is an inertial frame by neglecting its rotation. This simplification has allowed us to assume that the free-fall acceleration g of a particle is the same as the particle’s gravitational acceleration (which we now call a_g). Furthermore, we assumed that g has the constant value 9.8 m/s² any place on Earth’s surface. However, any g value measured at a given location will differ from the a_g value calculated with Eq. 13-11 for that location for three reasons: (1) Earth’s mass is not distributed uniformly, (2) Earth is not a perfect sphere, and (3) Earth rotates. Moreover, because g differs from a_g, the same three reasons mean that the measured weight mg of a particle differs from the magnitude of the gravitational force on the particle as given by Eq. 13-9. Let us now examine those reasons.

1.  Earth’s mass is not uniformly distributed. The density (mass per unit volume) of Earth varies radially as shown in Fig. 13-6, and the density of the crust (outer section) varies from region to region over Earth’s surface. Thus, g varies from region to region over the surface.

2.  Earth is not a sphere. Earth is approximately an ellipsoid, flattened at the poles and bulging at the equator. Its equatorial radius is greater than its polar radius by 21 km. Thus, a point at the poles is closer to the dense core of Earth than is a point on the equator. This is one reason the free-fall acceleration g increases as one proceeds, at sea level, from the equator toward either pole.

3.  Earth is rotating. The rotation axis runs through the north and south poles of Earth. An object located on Earth’s surface anywhere except at those poles must rotate in a circle about the rotation axis and thus must have a centripetal acceleration directed toward the center of the circle. This centripetal acceleration requires a centripetal net force that is also directed toward that center.

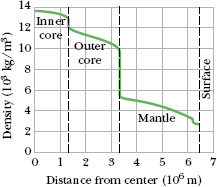
Fig. 13-6 The density of Earth as a function of distance from the center. The limits of the solid inner core, the largely liquid outer core, and the solid mantle are shown, but the crust of Earth is too thin to show clearly on this plot.

To see how Earth’s rotation causes g to differ from a_g, let us analyze a simple situation in which a crate of mass m is on a scale at the equator. Figure 13-7a shows this situation as viewed from a point in space above the north pole.

Figure 13-7b, a free-body diagram for the crate, shows the two forces on the crate, both acting along a radial r axis that extends from Earth’s center. The normal force  on the crate from the scale is directed outward, in the positive direction of the r axis. The gravitational force, represented with its equivalent m, is directed inward. Because it travels in a circle about the center of Earth as Earth turns, the crate has a centripetal acceleration  directed toward Earth’s center. From Eq. 10-23 (a_r = ω²r), we know this acceleration is equal to ω²R, where ω is Earth’s angular speed and R is the circle’s radius (approximately Earth’s radius). Thus, we can write Newton’s second law for forces along the r axis (F_net,r = ma_r) as

The magnitude F_N of the normal force is equal to the weight mg read on the scale. With mg substituted for F_N, Eq. 13-12 gives us

which says

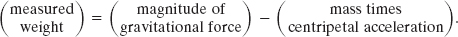
Thus, the measured weight is less than the magnitude of the gravitational force on the crate, because of Earth’s rotation.

To find a corresponding expression for g and a_g, we cancel m from Eq. 13-13 to write

which says

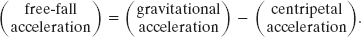
Thus, the measured free-fall acceleration is less than the gravitational acceleration because of Earth’s rotation.

The difference between accelerations g and a_g is equal to ω²R and is greatest on the equator (for one reason, the radius of the circle traveled by the crate is greatest there). To find the difference, we can use Eq. 10-5 (ω = Δθ/Δt) and Earth’s radius R = 6.37 × 10⁶ m. For one rotation of Earth, θ is 2π rad and the time period Δt is about 24 h. Using these values (and converting hours to seconds), we find that g is less than a_g by only about 0.034 m/s² (small compared to 9.8 m/s²). Therefore, neglecting the difference in accelerations g and a_g is often justified. Similarly, neglecting the difference between weight and the magnitude of the gravitational force is also often justified.

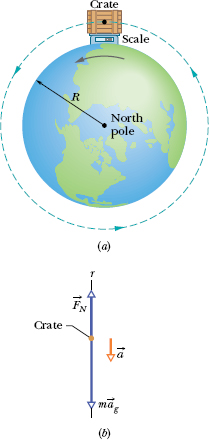
Fig. 13-7 (a) A crate sitting on a scale at Earth’s equator, as seen by an observer positioned on Earth’s rotation axis at some point above the north pole. (b) A free-body diagram for the crate, with a radial r axis extending from Earth’s center. The gravitational force on the crate is represented with its equivalent m. The normal force on the crate from the scale is . Because of Earth’s rotation, the crate has a centripetal acceleration  that is directed toward Earth’s center.

Sample Problem 13-3

(a) An astronaut whose height h is 1.70 m floats “feet down” in an orbiting space shuttle at distance r = 6.77 × 10⁶ m away from the center of Earth. What is the difference between the gravitational acceleration at her feet and at her head?

Solution: One Key Idea here is that we can approximate Earth as a uniform sphere of mass M_E. Then, from Eq. 13-11, the gravitational acceleration at any distance r from the center of Earth is

We might simply apply this equation twice, first with r = 6.77 × 10⁶ m for the feet and then with r = 6.77 × 10⁶ m + 1.70 m for the head. However, a calculator may give us the same value for a_g twice, and thus a difference of zero, because h is so much smaller than r. A second Key Idea helps here: Because we have a differential change dr in r between the astronaut’s feet and head, let us differentiate Eq. 13-15 with respect to r. That gives us

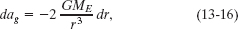
where da_g is the differential change in the gravitational acceleration due to the differential change dr in r. For the astronaut, dr = h and r = 6.77 × 10⁶ m. Substituting data into Eq. 13-16, we find

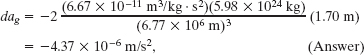
where the M_E value is taken from Appendix C. This result means that the gravitational acceleration of the astronaut’s feet toward Earth is slightly greater than the gravitational acceleration of her head toward Earth. This difference in acceleration tends to stretch her body, but the difference is so small that the stretching is unnoticeable.

(b) If the astronaut is now “feet down” at the same orbital radius r = 6.77 × 10⁶ m about a black hole of mass M_h = 1.99 × 10³¹ kg (10 times our Sun’s mass), what is the difference between the gravitational acceleration at her feet and at her head? The black hole has a mathematical surface (event horizon) of radius R_h = 2.95 × 10⁴ m. Nothing, not even light, can escape from that surface or anywhere inside it. Note that the astronaut is well outside the surface (at r = 229R_h).

Solution: The Key Idea here is that we again have a differential change dr in r between the astronaut’s feet and head, so we can again use Eq. 13-16. However, now we substitute M_h = 1.99 × 10³¹ kg for M_E. We find

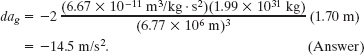
This means that the gravitational acceleration of the astronaut’s feet toward the black hole is noticeably larger than that of her head. The resulting tendency to stretch her body would be bearable but quite painful. If she drifted closer to the black hole, the stretching tendency would increase drastically.