The last class of concerted pericyclic reactions that we will consider is the groups of reactions known as sigmatropic rearrangements. In a sigmatropic rearrangement, a σ bond in a molecule is broken, a new σ bond is formed and the π electrons rearrange. The σ bond that breaks is bonded to an allylic carbon. It can be a σ bond between a carbon and hydrogen, between a carbon and another carbon, or between a carbon and an oxygen, nitrogen, or sulphur. ‘Sigmatropic’ comes from the Greek work tropos, which means, ‘change,’ so sigmatropic means ‘sigma-change’. The following points may be noted:
- The number of π bonds does not change; both the reactant and the product contain the same number of π bonds.
- The σ bond that cleaves can be in the middle of the π system or at the end of the π system.
- The σ bond that breaks is bonded to an allylic carbon.
- The numbering system used to describe a sigmatropic rearrangement [i, j] differs from any numbering system you have seen previously. First, mentally break the σ bond in the reactant into two pieces, and then assign number 1 to both the atoms involved in this bond. Then, the atoms in each direction from the bond being broken is counted in each of the fragments that connect the broken σ bond and the new σ bond. The two numbers are put in brackets with the small number stated first. For example, in the [2,3] sigmatropic rearrangement shown below, two atoms (N, N) connect the old and new σ bonds in one fragment and three atoms (C, C, C) connect the old and new σ bonds in the other fragment.
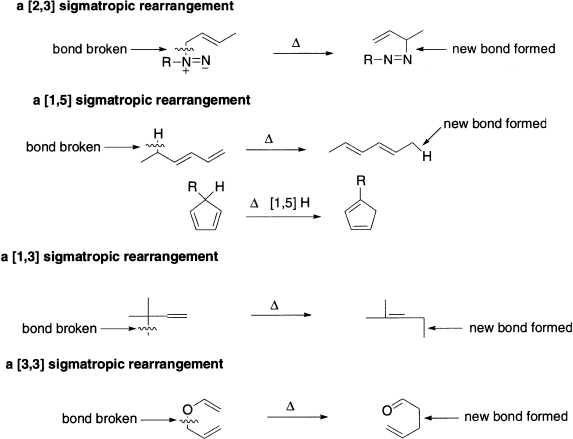
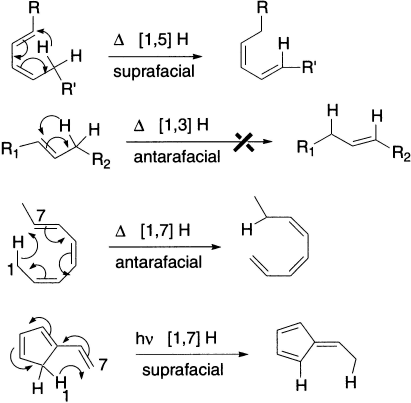
There are two different types of sigmatropic reactions, a) those that involve the migration of a hydrogen atom and b) those that involve a carbon or other atom. In the former category, the hydrogen atom can migrate either suprafacially or antarafacially across the conjugated system, leading to Huckel or Mobius topology for the transition states.
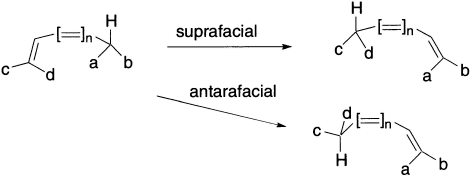
Something different can occur when a carbon migrates.
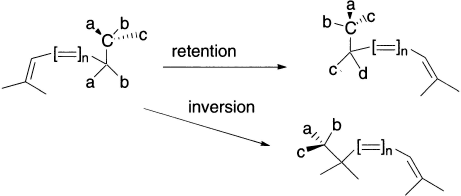
The configuration at the migrating centre can be either retained (= suprafacial mode = Huckel topology) or inverted (= antarafacial mode = Mobius topology). Note that Mobius transition states are relatively common in this class because there is often little strain involved in inversion of configuration at a carbon. The most common category of hydrogen shift involves a so called [1,5] sigmatropic shift.
In the transition state of a sigmatropic rearrangement, the group that migrates is partially bonded to the migration source and partially bonded to the migration terminus. There are two possible modes for rearrangement. If the migrating group remains on the same face of the π system, the rearrangement is suprafacial. If the migrating group moves to the opposite face of the π system, the rearrangement is antarafacial.
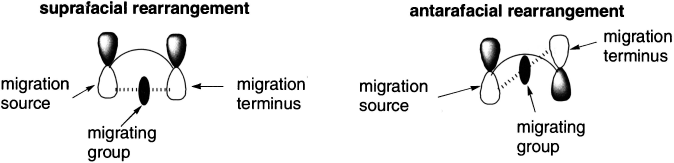
Sigmatropic rearrangements have cyclic transition states. If the transition state has six or fewer atoms in the ring, rearrangement must be suprafacial because of the geometric constraints of small rings.
Table 11.2 Woodward–Hoffmann Rules for Sigmatropic Rearrangements
| No. of pairs of electron in the reacting system | Reaction conditions | Allowed mode of ring closure |
|---|---|---|
| Even Number | Thermal Photochemical | Antarafaciala Suprafacial |
| Odd number | Thermal Photochemical | Suprafacial Antarafaciala |
a Although antrafacial ring closure is symmetry-allowed, it can occur only with large rings.
A [1,3] sigmatropic rearrangement involves a π bond and a pair of σ electrons, or we can say that it involves two pairs of electrons. A [1,5] sigmatropic rearrangement involves two π bonds and a pair of σ electrons (three pairs of electrons), and a [1,7] sigmatropic rearrangement involves four pairs of electrons. We can use the same symmetry rules for sigmatropic rearrangements that we used for cycloaddition reactions if we substitute ‘number of pairs of electrons’ for ‘sum of the number of π bonds.’ Recall that the ground-state HOMO of a compound with an even number of conjugated double bonds is asymmetric, but the ground-state HOMO of a compound with an odd number of conjugated double bonds is symmetric.
A Cope rearrangement is a [3,3] sigmatropic rearrangement of a 1,5-diene. A Claisen rearrangement is a [3,3] sigmatropic rearrangement of allyl vinyl ether. Both rearrangements form six-member ring transition states. Therefore, the reactions must be able to take place by a suprafacial pathway. Whether or not a suprafacial pathway is symmetry-allowed depends on the number of pairs of electrons involved in the rearrangement. Because [3,3] sigmatropic rearrangements involve three pairs of electrons, they occur by a suprafacial pathway under thermal conditions. Therefore, both Cope and Claisen rearrangements readily take place under thermal conditions.
Leave a Reply